समरूपता की धुरी क्या है? यह बिंदुओं का एक समूह है जो एक सीधी रेखा बनाता है, जो समरूपता का आधार है, अर्थात, यदि एक तरफ सीधी रेखा से एक निश्चित दूरी निर्धारित की जाती है, तो यह उसी आकार में दूसरी दिशा में परिलक्षित होगी।. कोई भी चीज एक धुरी के रूप में कार्य कर सकती है - एक बिंदु, एक रेखा, एक विमान, और इसी तरह। लेकिन इसके बारे में उदाहरण के साथ बात करना बेहतर है।
समरूपता
समरूपता की धुरी क्या है यह समझने के लिए, आपको समरूपता की परिभाषा में तल्लीन करने की आवश्यकता है। यह किसी भी धुरी के संबंध में शरीर के एक निश्चित टुकड़े का पत्राचार है, जब इसकी संरचना अपरिवर्तित होती है, और ऐसी वस्तु के गुण और आकार उसके परिवर्तनों के संबंध में समान रहते हैं। हम कह सकते हैं कि समरूपता प्रदर्शित करने के लिए निकायों की संपत्ति है। जब एक टुकड़े का ऐसा मेल नहीं हो सकता है, तो इसे विषमता या अतालता कहा जाता है।
कुछ आकृतियों में सममिति नहीं होती, इसलिए उन्हें अनियमित या असममित कहा जाता है। इनमें विभिन्न समलम्बाकार (समद्विबाहु को छोड़कर), त्रिभुज (समद्विबाहु और समबाहु को छोड़कर) और अन्य शामिल हैं।

समरूपता के प्रकार
हम इस अवधारणा का पूरी तरह से पता लगाने के लिए कुछ प्रकार की समरूपता पर भी चर्चा करेंगे। वे इस तरह विभाजित हैं:
- अक्षीय। समरूपता की धुरी शरीर के केंद्र से गुजरने वाली एक सीधी रेखा है। ऐशे ही? यदि आप समरूपता की धुरी के चारों ओर भागों को लगाते हैं, तो वे बराबर होंगे। इसे गोले के उदाहरण में देखा जा सकता है।
- दर्पण। यहां समरूपता की धुरी एक सीधी रेखा है, जिसके सापेक्ष शरीर परावर्तित हो सकता है और उलटा प्रदर्शित हो सकता है। उदाहरण के लिए, तितली के पंख दर्पण-सममित होते हैं।
- केंद्रीय। समरूपता की धुरी शरीर के केंद्र में वह बिंदु है, जिसके सापेक्ष, सभी परिवर्तनों के तहत, शरीर के अंग समान होते हैं जब आरोपित किया जाता है।
समरूपता का इतिहास
समरूपता की अवधारणा अक्सर प्राचीन वैज्ञानिकों के सिद्धांतों और परिकल्पनाओं में शुरुआती बिंदु है जो ब्रह्मांड के गणितीय सामंजस्य में विश्वास रखते थे, साथ ही साथ दैवीय सिद्धांत की अभिव्यक्ति में भी। प्राचीन यूनानियों का दृढ़ विश्वास था कि ब्रह्मांड सममित है, क्योंकि समरूपता शानदार है। मनुष्य ने लंबे समय से ब्रह्मांड के चित्र के अपने ज्ञान में समरूपता के विचार का उपयोग किया है।
ईसा पूर्व 5वीं शताब्दी में, पाइथागोरस ने गोले को सबसे उत्तम रूप माना और सोचा कि पृथ्वी एक गोले के आकार की है और उसी तरह चलती है। उनका यह भी मानना था कि पृथ्वी किसी प्रकार की "केंद्रीय अग्नि" के रूप में घूमती है, जिसके चारों ओर 6 ग्रह (उस समय ज्ञात), चंद्रमा, सूर्य और अन्य सभी सितारों को घूमना चाहिए था।
और दार्शनिक प्लेटो ने पॉलीहेड्रॉन को चार प्राकृतिक तत्वों का अवतार माना:
- टेट्राहेड्रॉन आग है, इसके शीर्ष के रूप मेंइशारा करना;
- घन - पृथ्वी, क्योंकि यह सबसे स्थिर पिंड है;
- ऑक्टाहेड्रोन - हवा, कोई स्पष्टीकरण नहीं;
- icosahedron - पानी, क्योंकि शरीर में खुरदुरी ज्यामितीय आकृतियाँ, कोण आदि नहीं होते हैं;
- पूरे ब्रह्मांड की छवि डोडेकाहेड्रोन थी।
इन सभी सिद्धांतों के कारण, नियमित पॉलीहेड्रा को प्लेटोनिक ठोस कहा जाता है।
समरूपता का प्रयोग प्राचीन ग्रीस के वास्तुकारों द्वारा किया जाता था। उनकी सभी इमारतें सममित थीं, जैसा कि ओलंपिया में ज़ीउस के प्राचीन मंदिर की छवियों से पता चलता है।

डच कलाकार एम.सी. एस्चर ने भी अपने चित्रों में समरूपता का प्रयोग किया है। विशेष रूप से, दो पक्षियों की एक मोज़ेक की ओर उड़ते हुए "दिन और रात" पेंटिंग का आधार बन गया।
इसके अलावा, हमारे कला समीक्षकों ने समरूपता के नियमों की उपेक्षा नहीं की, जैसा कि वासंतोसेव वी.एम. "हीरोज" की पेंटिंग के उदाहरण में देखा जा सकता है।
मैं क्या कह सकता हूं, समरूपता कई सदियों से सभी कलाकारों के लिए एक प्रमुख अवधारणा रही है, लेकिन 20वीं शताब्दी में सटीक विज्ञान के सभी आंकड़ों द्वारा इसके अर्थ की सराहना की गई थी। सटीक प्रमाण भौतिक और ब्रह्माण्ड संबंधी सिद्धांत हैं, उदाहरण के लिए, सापेक्षता का सिद्धांत, स्ट्रिंग सिद्धांत, बिल्कुल सभी क्वांटम यांत्रिकी। प्राचीन बेबीलोन के समय से लेकर आधुनिक विज्ञान की अत्याधुनिक खोजों के अंत तक, समरूपता के अध्ययन और इसके मूल नियमों की खोज के रास्तों का पता लगाया जा सकता है।
ज्यामितीय आकृतियों और निकायों की समरूपता
आइए ज्यामितीय निकायों पर करीब से नज़र डालते हैं। उदाहरण के लिए, एक परवलय की सममिति की धुरी उसके शीर्ष से गुजरने वाली और दिए गए पिंड को काटने वाली एक सीधी रेखा है।आधे में। इस आकृति में एक एकल अक्ष है।
लेकिन ज्यामितीय आकृतियों के साथ स्थिति अलग है। आयत की सममिति की धुरी भी सीधी है, लेकिन उनमें से कई हैं। आप चौड़ाई के खंडों के समानांतर एक अक्ष खींच सकते हैं, या आप लंबाई खींच सकते हैं। लेकिन सब कुछ इतना आसान नहीं है। यहाँ रेखा में सममिति का कोई अक्ष नहीं है, क्योंकि इसका अंत परिभाषित नहीं है। केवल केंद्रीय समरूपता मौजूद हो सकती है, लेकिन, तदनुसार, एक भी नहीं होगी।
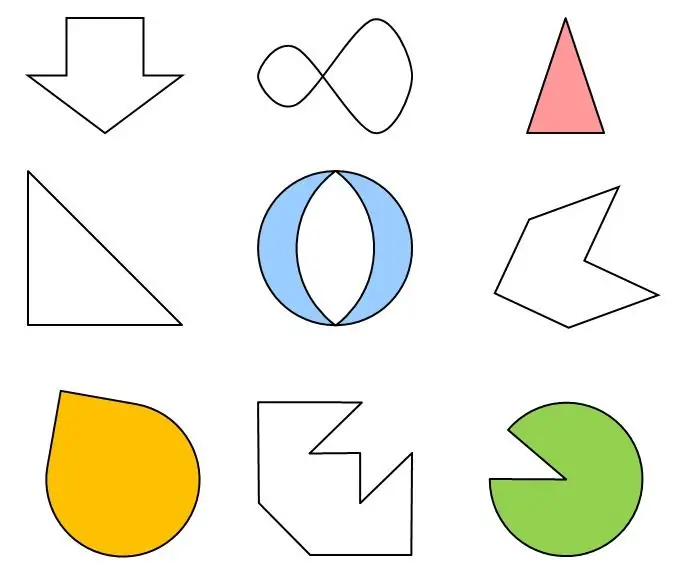
आपको यह भी पता होना चाहिए कि कुछ निकायों में समरूपता के कई अक्ष होते हैं। यह अनुमान लगाना आसान है। आपको इस बारे में बात करने की भी आवश्यकता नहीं है कि एक वृत्त में कितनी सममिति की कुल्हाड़ियाँ हैं। वृत्त के केंद्र से गुजरने वाली कोई भी रेखा ऐसी होती है, और इन रेखाओं की संख्या अनंत होती है।
कुछ चतुर्भुजों में सममिति के दो अक्ष हो सकते हैं। लेकिन दूसरा लंबवत होना चाहिए। यह समचतुर्भुज और आयत के मामले में होता है। समरूपता की पहली धुरी में - विकर्ण, और दूसरे में - मध्य रेखाएँ। ऐसी कुल्हाड़ियों का समुच्चय केवल वर्ग के लिए होता है।
प्रकृति में समरूपता
समरूपता के कई उदाहरणों से प्रकृति हैरान है। हमारा मानव शरीर भी सममित है। चेहरे की केंद्रीय धुरी के बारे में दो आंखें, दो कान, नाक और मुंह सममित रूप से स्थित हैं। हाथ, पैर और पूरे शरीर को सामान्य रूप से हमारे शरीर के मध्य से गुजरने वाली धुरी पर सममित रूप से व्यवस्थित किया जाता है।

और कितने ही उदाहरण हमें हर समय घेरे रहते हैं! ये फूल, पत्ते, पंखुड़ियाँ, सब्जियाँ और फल, जानवर और यहाँ तक कि मधुमक्खियों के छत्ते भी एक स्पष्ट ज्यामितीय आकार और समरूपता रखते हैं। सभी प्रकृतिव्यवस्थित ढंग से व्यवस्थित, हर चीज का अपना स्थान होता है, जो एक बार फिर प्रकृति के नियमों की पूर्णता की पुष्टि करता है, जिसमें समरूपता मुख्य शर्त है।
निष्कर्ष
हम लगातार कुछ घटनाओं और वस्तुओं से घिरे रहते हैं, जैसे कि एक इंद्रधनुष, एक बूंद, फूल, पंखुड़ी, आदि। उनकी समरूपता स्पष्ट है, कुछ हद तक यह गुरुत्वाकर्षण के कारण है। अक्सर प्रकृति में, "समरूपता" की अवधारणा को दिन और रात, ऋतुओं आदि के नियमित परिवर्तन के रूप में समझा जाता है।

जहाँ भी व्यवस्था और समानता होती है, वहाँ समान गुण देखे जाते हैं। इसके अलावा, प्रकृति के बहुत ही नियम - खगोलीय, रासायनिक, जैविक और यहां तक कि आनुवंशिक - समरूपता के कुछ सिद्धांतों के अधीन हैं, क्योंकि उनके पास एक आदर्श प्रणाली है, जिसका अर्थ है कि संतुलन में एक सर्वव्यापी पैमाना है। इसलिए, अक्षीय समरूपता समग्र रूप से ब्रह्मांड के मूलभूत नियमों में से एक है।






