किसी भी वैज्ञानिक क्षेत्र और ज्ञान के क्षेत्र में, ऐसी घटनाएं होती हैं, जिनका अध्ययन किसी विशेष समय अवधि में सभी परिवर्तनों को ध्यान में रखते हुए करना उचित है। जहां तक किसी व्यक्ति के दैनिक वातावरण का सवाल है, तो यह उसके लिए रुचिकर है, उदाहरण के लिए, पिछले एक साल में किसी विशेष उत्पाद की कीमतों में कैसे बदलाव आया है, जैसा कि चिकित्सा क्लीनिकों में नियमित परीक्षाओं से पता चलता है, आदि।

आंकड़ों में, एक निश्चित अवधि में एक या किसी अन्य वस्तु के साथ होने वाले परिवर्तनों की समग्रता एक समय श्रृंखला के अलावा और कुछ नहीं है। इस विशेषता का कोई भी स्तर एक समय या किसी अन्य पर कई कारकों से प्रभावित होता है, जिनमें से प्रत्येक को या तो यादृच्छिक या सिस्टम बनाने वाले क्षणों के लिए जिम्मेदार ठहराया जा सकता है जो अल्पकालिक प्रवृत्ति और चक्रीय उतार-चढ़ाव दोनों को प्रभावित करते हैं।
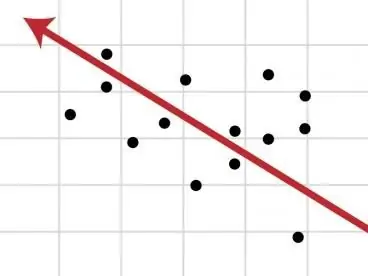
इन कारकों के विभिन्न संयोजनों का विश्लेषण करते हुए, हम यह निष्कर्ष निकाल सकते हैं कि किसी विशेष क्षेत्र के आधार पर समय श्रृंखला निम्नलिखित में से एक रूप ले सकती है। सबसे पहले,आर्थिक संकेतकों का एक महत्वपूर्ण हिस्सा, मैक्रो- और माइक्रो-लेवल दोनों, निरंतर गतिशील परिवर्तन में है, क्योंकि वे बड़ी संख्या में कारकों से प्रभावित होते हैं। साथ ही, इस तथ्य के बावजूद कि इन कारकों को अक्सर अलग-अलग दिशाओं में निर्देशित किया जाता है, उनकी समग्रता में वे एक यूनिडायरेक्शनल प्रवृत्ति बनाते हैं, जो किसी विशेष संकेतक के विकास में प्रगति या प्रतिगमन दिखाते हैं।
दूसरा, एक या दूसरे संकेतक द्वारा समय श्रृंखला को देखते हुए, कोई स्पष्ट रूप से देख सकता है कि यह ध्यान देने योग्य चक्रीय उतार-चढ़ाव के अधीन है। यह मौसमों के परिवर्तन, वैश्विक रुझानों या कुछ नौकरियों के चक्र की अवधि के कारण हो सकता है।

यह पता लगाने के लिए कि किसी समय श्रृंखला में किसी विशेष समय पर वास्तविक विशेषता क्या होती है, इसकी यादृच्छिक प्रवृत्ति और चक्रीय घटकों को जोड़ना या गुणा करना आवश्यक है। जोड़ के परिणामस्वरूप प्राप्त परिणाम समय श्रृंखला का एक योगात्मक मॉडल होगा, और यदि गुणन लागू किया जाता है, तो परिणाम एक गुणक मॉडल होगा।
किसी भी सांख्यिकीय अध्ययन का मुख्य कार्य किसी विशेष समय श्रृंखला के सभी तीन मुख्य घटकों के मात्रात्मक संकेतकों को निर्धारित करना है। इस श्रृंखला के मूल्यों की भविष्यवाणी करने के लिए यह आवश्यक है जो भविष्य में हमसे उम्मीद कर सकते हैं।
कई मामलों में, वैज्ञानिकों को लगभग समान समय अंतराल पर एक निश्चित संख्या में अवलोकनों का नमूना लेने की आवश्यकता होती है, अर्थात एक स्थिर समय श्रृंखला होती है। वहउन मामलों में प्राप्त किया जाता है जब प्रवृत्ति को गतिशील समय श्रृंखला से हटा दिया जाता है, अर्थात वे कारक जिनकी सहायता से अल्पकालिक प्रवृत्तियों का निर्माण होता है।
इस प्रकार, एक समय श्रृंखला एक निश्चित समय अवधि में लिए गए एक या दूसरे संकेतक के मात्रात्मक मूल्यों का एक सेट है। प्रत्येक स्तर का गठन कई कारकों से प्रभावित होता है, दोनों अल्पकालिक और दीर्घकालिक।






