ओम का नियम विद्युत परिपथों का मूल नियम है। साथ ही, यह हमें कई प्राकृतिक घटनाओं की व्याख्या करने की अनुमति देता है। उदाहरण के लिए, कोई यह समझ सकता है कि बिजली तारों पर बैठने वाले पक्षियों को "धड़क" क्यों नहीं देती। भौतिकी के लिए ओम का नियम अत्यंत महत्वपूर्ण है। उनकी जानकारी के बिना, स्थिर विद्युत सर्किट बनाना असंभव होगा या कोई इलेक्ट्रॉनिक्स बिल्कुल भी नहीं होगा।
निर्भरता I=I(U) और उसका मान
सामग्री के प्रतिरोध की खोज का इतिहास सीधे वर्तमान-वोल्टेज विशेषता से संबंधित है। यह क्या है? आइए एक निरंतर विद्युत प्रवाह के साथ एक सर्किट लें और इसके किसी भी तत्व पर विचार करें: एक दीपक, एक गैस पाइप, एक धातु कंडक्टर, एक इलेक्ट्रोलाइट फ्लास्क, आदि।
संदर्भित तत्व को आपूर्ति किए गए वोल्टेज यू (अक्सर वी के रूप में संदर्भित) को बदलना, हम इसके माध्यम से गुजरने वाले वर्तमान (आई) की ताकत में परिवर्तन को ट्रैक करेंगे। नतीजतन, हमें फॉर्म I \u003d I (U) की निर्भरता मिलेगी, जिसे "तत्व की वोल्टेज विशेषता" कहा जाता है और इसका प्रत्यक्ष संकेतक हैविद्युत गुण।
V/A विशेषता विभिन्न तत्वों के लिए भिन्न दिख सकती है। इसका सरलतम रूप एक धातु कंडक्टर पर विचार करके प्राप्त किया जाता है, जो जॉर्ज ओम (1789 - 1854) द्वारा किया गया था।
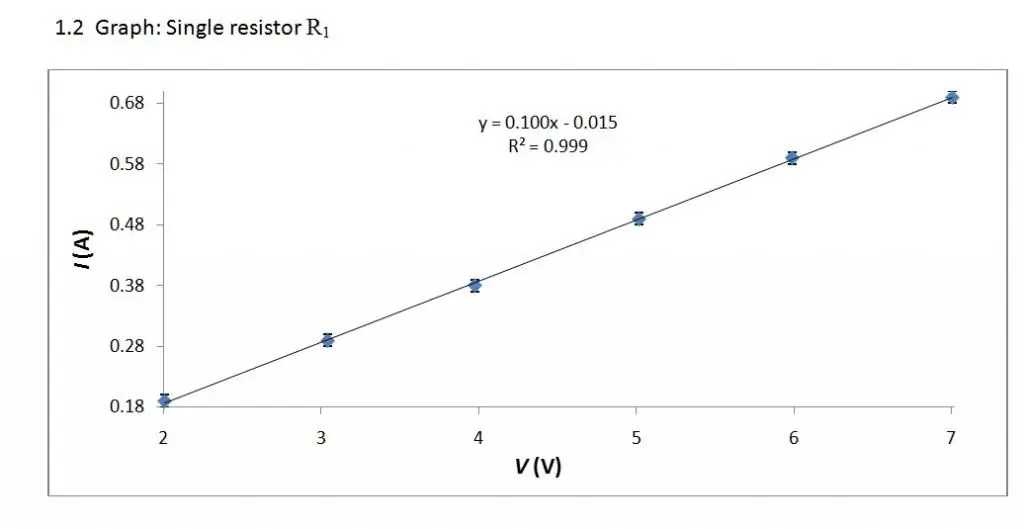
वोल्ट-एम्पीयर विशेषता एक रैखिक संबंध है। अत: इसका आलेख एक सरल रेखा है।
कानून अपने सरलतम रूप में
कंडक्टरों की करंट-वोल्टेज विशेषताओं पर ओम के शोध से पता चला है कि एक धातु कंडक्टर के अंदर की वर्तमान ताकत उसके सिरों (I ~ U) पर संभावित अंतर के समानुपाती होती है और एक निश्चित गुणांक के व्युत्क्रमानुपाती होती है, अर्थात I ~ 1 / आर। यह गुणांक "कंडक्टर प्रतिरोध" के रूप में जाना जाने लगा, और विद्युत प्रतिरोध के मापन की इकाई ओम या वी/ए थी।
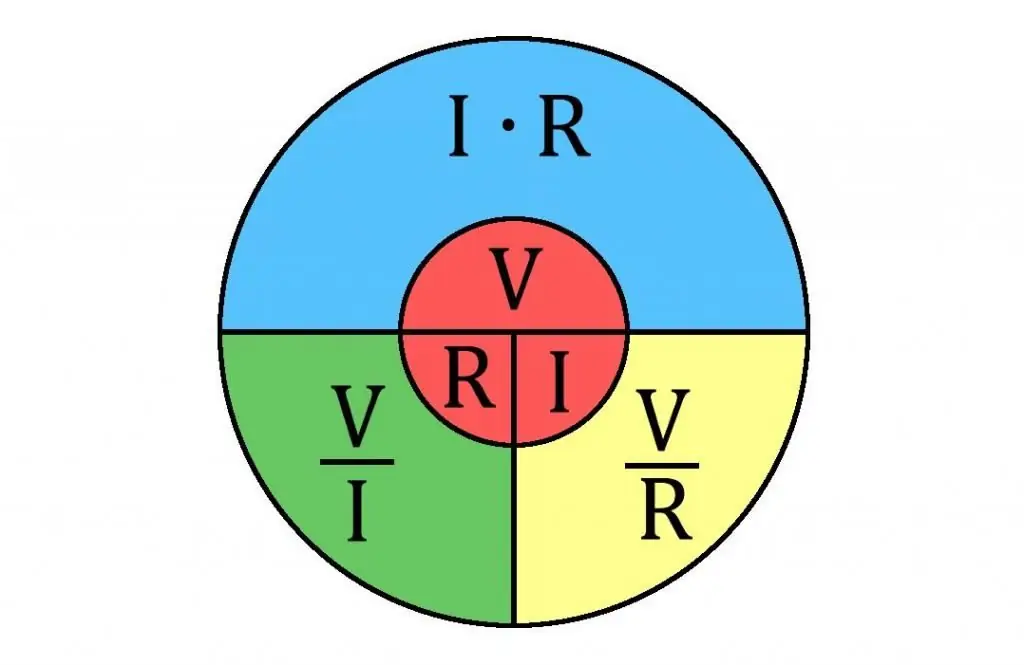
एक और बात ध्यान देने वाली है। सर्किट में प्रतिरोध की गणना के लिए अक्सर ओम के नियम का उपयोग किया जाता है।
कानूनी शब्द
ओम का नियम कहता है कि सर्किट के एक खंड की वर्तमान ताकत (I) इस खंड में वोल्टेज के समानुपाती होती है और इसके प्रतिरोध के व्युत्क्रमानुपाती होती है।
यह ध्यान दिया जाना चाहिए कि इस रूप में कानून केवल श्रृंखला के एक सजातीय खंड के लिए सही रहता है। सजातीय विद्युत परिपथ का वह भाग है जिसमें धारा स्रोत नहीं होता है। एक अमानवीय परिपथ में ओम के नियम का उपयोग कैसे करें नीचे चर्चा की जाएगी।
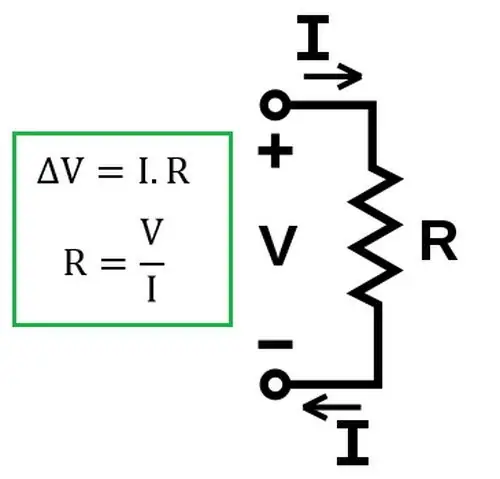
बाद में, यह प्रयोगात्मक रूप से स्थापित किया गया था कि कानून समाधान के लिए वैध रहता हैविद्युत परिपथ में इलेक्ट्रोलाइट्स।
प्रतिरोध का भौतिक अर्थ
प्रतिरोध विद्युत धारा के पारित होने को रोकने के लिए सामग्री, पदार्थों या मीडिया का एक गुण है। मात्रात्मक रूप से, 1 ओम के प्रतिरोध का अर्थ है कि एक कंडक्टर में जिसके सिरों पर 1 V का वोल्टेज है, 1 A का विद्युत प्रवाह गुजर सकता है।
विद्युत प्रतिरोधकता
प्रयोगात्मक रूप से, यह पाया गया कि कंडक्टर के विद्युत प्रवाह का प्रतिरोध उसके आयामों पर निर्भर करता है: लंबाई, चौड़ाई, ऊंचाई। और इसके आकार (गोलाकार, बेलन) और जिस सामग्री से इसे बनाया जाता है उस पर भी। इस प्रकार, प्रतिरोधकता का सूत्र, उदाहरण के लिए, एक सजातीय बेलनाकार कंडक्टर का होगा: आर \u003d पीएल / एस।
यदि इस सूत्र में हम s=1 m2 और l=1 m डालते हैं, तो R संख्यात्मक रूप से p के बराबर होगा। यहाँ से, SI में कंडक्टर की प्रतिरोधकता के गुणांक के लिए माप की इकाई की गणना की जाती है - यह ओमm है।

प्रतिरोधकता सूत्र में, पी उस सामग्री के रासायनिक गुणों द्वारा निर्धारित प्रतिरोध गुणांक है जिससे कंडक्टर बनाया जाता है।
ओम के नियम के विभेदक रूप पर विचार करने के लिए, हमें कुछ और अवधारणाओं पर विचार करने की आवश्यकता है।
वर्तमान घनत्व
जैसा कि आप जानते हैं, विद्युत प्रवाह किसी भी आवेशित कणों की एक कड़ाई से क्रमबद्ध गति है। उदाहरण के लिए, धातुओं में, वर्तमान वाहक इलेक्ट्रॉन होते हैं, और गैसों के संचालन में, आयन।
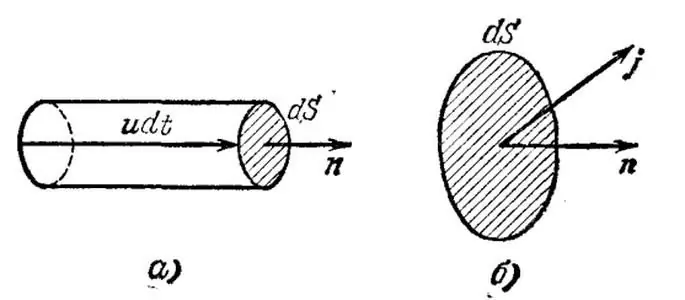
मामूली मामला लें जब सभी मौजूदा वाहकसजातीय - धातु कंडक्टर। आइए हम मानसिक रूप से इस चालक में एक असीम रूप से छोटे आयतन को अलग करें और दिए गए आयतन में इलेक्ट्रॉनों के औसत (बहाव, क्रमित) वेग को यू द्वारा निरूपित करें। इसके अलावा, n प्रति इकाई आयतन में वर्तमान वाहकों की सांद्रता को निरूपित करते हैं।
अब चलो वेक्टर u के लंबवत क्षेत्र dS ड्रा करते हैं और वेग के साथ udt ऊंचाई के साथ एक इनफिनिटिमल सिलेंडर का निर्माण करते हैं, जहां dt उस समय को दर्शाता है जिसके दौरान माना मात्रा में निहित सभी वर्तमान वेग वाहक गुजरेंगे क्षेत्र के माध्यम से डीएस
इस मामले में, q=neudSdt के बराबर चार्ज इलेक्ट्रॉनों द्वारा उस क्षेत्र में स्थानांतरित किया जाएगा, जहां ई इलेक्ट्रॉन चार्ज है। इस प्रकार, विद्युत धारा घनत्व एक सदिश j=neu है, जो एक इकाई क्षेत्र के माध्यम से प्रति इकाई समय में स्थानांतरित आवेश की मात्रा को दर्शाता है।
ओम के नियम अंतर परिभाषा के लाभों में से एक यह है कि आप अक्सर प्रतिरोध की गणना किए बिना प्राप्त कर सकते हैं।
इलेक्ट्रिक चार्ज। विद्युत क्षेत्र की ताकत
विद्युत के सिद्धांत में विद्युत आवेश के साथ-साथ क्षेत्र की ताकत एक मूलभूत पैरामीटर है। साथ ही, स्कूली बच्चों के लिए उपलब्ध सरल प्रयोगों से उनका मात्रात्मक विचार प्राप्त किया जा सकता है।
सरलता के लिए, हम एक स्थिरवैद्युत क्षेत्र पर विचार करेंगे। यह एक विद्युत क्षेत्र है जो समय के साथ नहीं बदलता है। ऐसा क्षेत्र स्थिर विद्युत आवेशों द्वारा बनाया जा सकता है।
साथ ही, हमारे उद्देश्यों के लिए एक परीक्षण शुल्क की आवश्यकता है। इसकी क्षमता में हम एक आवेशित शरीर का उपयोग करेंगे - इतना छोटा कि यह पैदा करने में सक्षम नहीं हैआस-पास की वस्तुओं में कोई गड़बड़ी (आवेशों का पुनर्वितरण)।
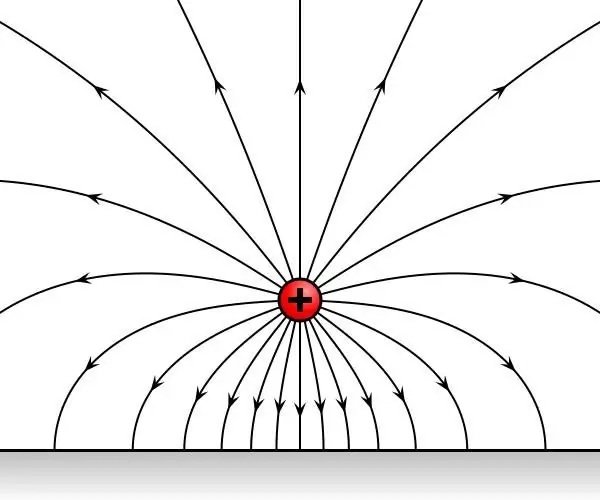
आइए बदले में लिए गए दो परीक्षण शुल्कों पर विचार करें, जो अंतरिक्ष में एक बिंदु पर क्रमिक रूप से रखे गए हैं, जो एक इलेक्ट्रोस्टैटिक क्षेत्र के प्रभाव में है। यह पता चला है कि आरोपों को उसकी ओर से समय-अपरिवर्तनीय प्रभाव के अधीन किया जाएगा। चलो F1 और F2 आरोपों पर कार्य करने वाले बल हैं।
प्रयोगात्मक डेटा के सामान्यीकरण के परिणामस्वरूप, यह पाया गया कि F1 और F2 बल या तो एक में निर्देशित हैं या विपरीत दिशाओं में, और उनका अनुपात F1/F2 अंतरिक्ष में उस बिंदु से स्वतंत्र है जहां परीक्षण शुल्क वैकल्पिक रूप से रखे गए थे। इसलिए, अनुपात F1/F2 स्वयं आरोपों की एक विशेषता है, और यह क्षेत्र पर निर्भर नहीं करता है।
इस तथ्य की खोज ने निकायों के विद्युतीकरण को चिह्नित करना संभव बना दिया और बाद में इसे विद्युत आवेश कहा गया। इस प्रकार, परिभाषा के अनुसार, यह q1/q2=F1/F निकलता है 2 , जहां q1 और q2 - क्षेत्र के एक बिंदु पर लगाए गए शुल्कों की राशि, और F 1 और F2 - मैदान की ओर से आवेशों पर कार्य करने वाले बल।
ऐसे विचारों से, विभिन्न कणों के आवेशों के परिमाण को प्रयोगात्मक रूप से स्थापित किया गया था। अनुपात में एक के बराबर परीक्षण शुल्कों में से एक को सशर्त रूप से सेट करके, आप F1/F2 के अनुपात को मापकर दूसरे शुल्क के मूल्य की गणना कर सकते हैं।.
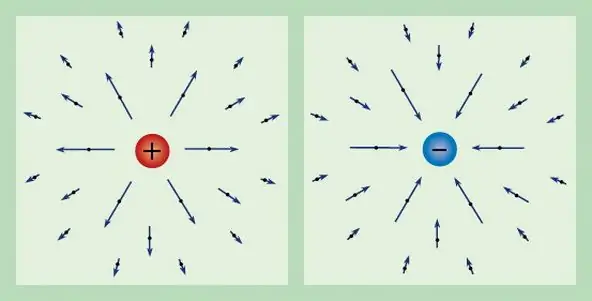
किसी भी विद्युत क्षेत्र को ज्ञात आवेश द्वारा अभिलक्षित किया जा सकता है। इस प्रकार, एक इकाई परीक्षण आवेश पर आराम करने वाले बल को विद्युत क्षेत्र की शक्ति कहा जाता है और इसे E द्वारा दर्शाया जाता है। आवेश की परिभाषा से, हम प्राप्त करते हैं कि शक्ति वेक्टर का निम्नलिखित रूप है: E=F/q.
सदिशों का संयोजन j और E. ओम के नियम का दूसरा रूप
एक समांगी चालक में आवेशित कणों की क्रमबद्ध गति सदिश E की दिशा में होगी। इसका अर्थ है कि सदिश j और E सह-निर्देशित होंगे। वर्तमान घनत्व का निर्धारण करने के लिए, हम कंडक्टर में एक असीम रूप से छोटे बेलनाकार आयतन का चयन करते हैं। फिर jdS के बराबर एक करंट इस सिलेंडर के क्रॉस सेक्शन से होकर गुजरेगा, और सिलेंडर पर लगाया जाने वाला वोल्टेज Edl के बराबर होगा। बेलन की प्रतिरोधकता का सूत्र भी ज्ञात है।
फिर, वर्तमान ताकत के लिए सूत्र को दो तरह से लिखने पर, हमें मिलता है: j=E/p, जहां मान 1/p को विद्युत चालकता कहा जाता है और विद्युत प्रतिरोधकता का व्युत्क्रम होता है। इसे आमतौर पर (सिग्मा) या λ (लैम्ब्डा) के रूप में दर्शाया जाता है। चालकता की इकाई एसएम/एम है, जहां एसएम सीमेंस है। ओम का मात्रक व्युत्क्रम।
इस प्रकार, हम एक अमानवीय सर्किट के लिए ओम के नियम के बारे में ऊपर दिए गए प्रश्न का उत्तर दे सकते हैं। इस मामले में, वर्तमान वाहक इलेक्ट्रोस्टैटिक क्षेत्र से बल से प्रभावित होंगे, जो कि तीव्रता E1 द्वारा विशेषता है, और अन्य बल उन पर किसी अन्य वर्तमान स्रोत से कार्य करते हैं, जो हो सकता है नामित ई 2। तब ओम का नियम लागू होता हैश्रृंखला का अमानवीय खंड इस तरह दिखेगा: j=(E1 + E2)।
चालकता और प्रतिरोध के बारे में अधिक
विद्युत प्रवाह का संचालन करने के लिए एक कंडक्टर की क्षमता इसकी प्रतिरोधकता की विशेषता है, जिसे प्रतिरोधकता सूत्र, या चालकता के माध्यम से पाया जा सकता है, जिसे चालकता के पारस्परिक के रूप में गणना की जाती है। इन मापदंडों का मूल्य कंडक्टर सामग्री के रासायनिक गुणों और बाहरी स्थितियों दोनों द्वारा निर्धारित किया जाता है। विशेष रूप से, परिवेश का तापमान।
अधिकांश धातुओं के लिए, सामान्य तापमान पर प्रतिरोधकता इसके समानुपाती होती है, अर्थात p ~ T. हालांकि, कम तापमान पर विचलन देखा जाता है। 0°K के करीब तापमान पर बड़ी संख्या में धातुओं और मिश्र धातुओं के लिए, प्रतिरोध गणना ने शून्य मान दिखाया। इस घटना को अतिचालकता कहा जाता है। उदाहरण के लिए, पारा, टिन, सीसा, एल्युमिनियम आदि में यह गुण होता है। प्रत्येक धातु का अपना महत्वपूर्ण तापमान Tk होता है, जिस पर अतिचालकता की घटना देखी जाती है।
यह भी ध्यान दें कि सिलेंडर प्रतिरोधकता की परिभाषा को उसी सामग्री से बने तारों के लिए सामान्यीकृत किया जा सकता है। इस मामले में, प्रतिरोधकता सूत्र से क्रॉस-सेक्शनल क्षेत्र तार के क्रॉस सेक्शन के बराबर होगा, और एल - इसकी लंबाई।






