कक्षा 10 में भौतिकी का अध्ययन करते समय द्विध्रुव के विषय पर विचार किया जाता है। इस अवधारणा का क्या अर्थ है और इसकी गणना के लिए किन सूत्रों का उपयोग किया जाता है?
परिचय
यदि आप एकसमान विद्युत क्षेत्र के स्थान में द्विध्रुव रखते हैं, तो आप इसे बल रेखाओं के रूप में निरूपित कर सकते हैं। द्विध्रुव एक प्रणाली है जिसमें दो आवेश होते हैं जो मापदंडों में समान होते हैं, लेकिन वे विपरीत बिंदु आवेश होते हैं। इसके अलावा, उनके बीच की दूरी द्विध्रुवीय क्षेत्र के किसी भी बिंदु की दूरी से बहुत कम होगी। विद्युतगतिकी (ग्रेड 10) के स्कूल पाठ्यक्रम में द्विध्रुवीय क्षण की अवधारणा का अध्ययन किया जाता है।
द्विध्रुव की धुरी एक सीधी रेखा है जो दोनों आवेशों के बिंदुओं से होकर गुजरती है। एक द्विध्रुवीय भुजा एक वेक्टर है जो एक चार्ज को जोड़ता है और साथ ही साथ नकारात्मक चार्ज कणों से सकारात्मक चार्ज कणों तक जाता है। एक विद्युत द्विध्रुव को ऐसी अवस्था की उपस्थिति के रूप में एक द्विध्रुवीय या विद्युत क्षण की विशेषता है।
परिभाषा के अनुसार, एक द्विध्रुवीय क्षण एक सदिश है जो संख्यात्मक रूप से द्विध्रुवीय आवेश और उसकी भुजा के गुणनफल के बराबर होता है। इसके अलावा, यह द्विध्रुव के कंधे के साथ सह-निर्देशित है। बलों के योग की शून्य समानता पर, हम क्षण के मूल्य की गणना करते हैं। उस कोण के लिए जो द्विध्रुव आघूर्ण और. के बीच मौजूद हैविद्युत क्षेत्र की दिशात्मकता, एक यांत्रिक क्षण की उपस्थिति विशेषता है।
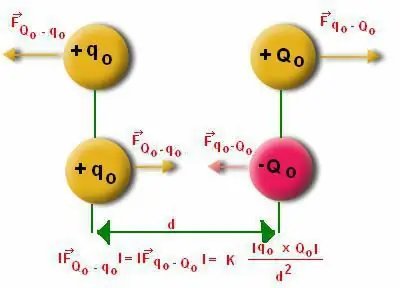
अक्सर लोगों को द्विध्रुव संरचना पर कार्य करने वाले मापांक की गणना करने में कठिनाई होती है। यहां "अल्फा" कोण की गणना करने की ख़ासियत को ध्यान में रखना आवश्यक है। यह ज्ञात है कि द्विध्रुव संतुलित स्थिति से विचलित होता है। लेकिन द्विध्रुवीय क्षण में ही एक पुनर्स्थापना चरित्र होता है, क्योंकि यह गति में रहता है।
गणना
जब यह द्विध्रुव आघूर्ण एक अमानवीय विद्युत क्षेत्र के माध्यम में रखा जाता है, तो अनिवार्य रूप से एक बल उत्पन्न होता है। ऐसे वातावरण में बलों के योग के संकेतक शून्य नहीं होंगे। नतीजतन, एक बिंदु चरित्र के साथ द्विध्रुवीय क्षण पर कार्य करने वाले बल होते हैं। द्विध्रुवीय भुजा का आकार बहुत छोटा होता है।
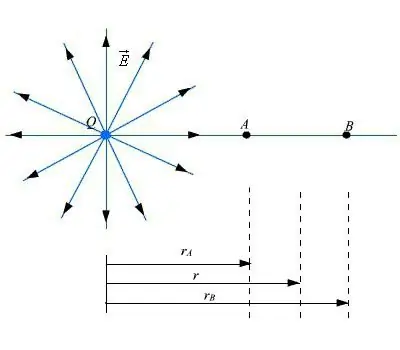
सूत्र को इस तरह लिखा जा सकता है: F=q (E2 - E1)=qdE, जहां d विद्युत क्षेत्र का अंतर है।
अध्ययन के तहत भौतिक अवधारणा की विशेषताओं की खोज करें
आइए आगे विषय पर नजर डालते हैं। यह निर्धारित करने के लिए कि विद्युत क्षेत्र की विशेषता क्या है, यदि इसे आवेशों की एक प्रणाली का उपयोग करके बनाया गया है और एक छोटी सी जगह में स्थानीयकृत किया गया है, तो कई गणना करना आवश्यक है। एक उदाहरण परमाणुओं और अणुओं द्वारा प्रस्तुत किया जाता है, जिनकी संरचना में विद्युत आवेशित नाभिक और इलेक्ट्रॉन होते हैं।
यदि कण स्थित क्षेत्र को बनाने वाले आयामों से अधिक दूरी पर एक क्षेत्र की खोज करना आवश्यक है, तो हम कई सटीक सूत्रों का उपयोग करेंगे जो अत्यधिक जटिल हैं। सरल का उपयोग करना संभव हैअनुमानित अभिव्यक्तियाँ। आइए मान लें कि आवेशों के बिंदु सेट qk विद्युत क्षेत्र के निर्माण में भाग लेते हैं। वे एक छोटी सी जगह में स्थित हैं।
फ़ील्ड की विशेषता की गणना करने के लिए, इसे सिस्टम के सभी शुल्कों को संयोजित करने की अनुमति है। इस तरह की प्रणाली को एक बिंदु आवेश Q के रूप में माना जाता है। परिमाण संकेतक उन शुल्कों का योग होगा जो मूल प्रणाली में थे।
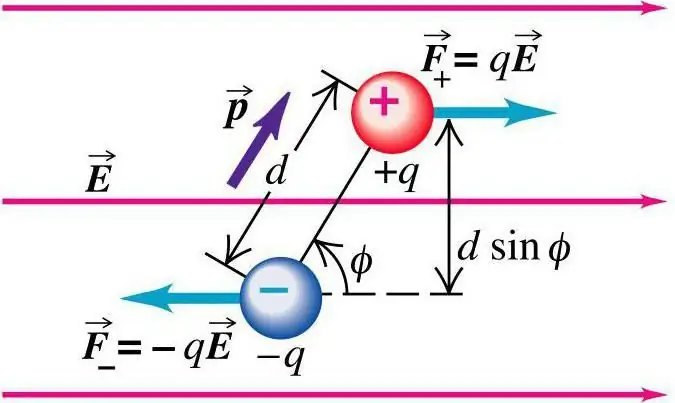
शुल्क का स्थान
आइए कल्पना करें कि चार्ज का स्थान किसी भी स्थान पर इंगित किया गया है जहां चार्ज सिस्टम qk स्थित है। स्थान में परिवर्तन करते समय, यदि इसकी सीमाएँ एक छोटे से क्षेत्र में व्यक्त की गई हैं, तो ऐसा प्रभाव नगण्य होगा, देखने के बिंदु पर क्षेत्र के लिए लगभग अगोचर। शक्ति और क्षमता के अनुमान की ऐसी सीमा के भीतर, जो विद्युत क्षेत्र में है, पारंपरिक सूत्रों का उपयोग करके निर्धारण किया जाता है।
जब सिस्टम के कुल चार्ज का योग शून्य होता है, तो संकेतित सन्निकटन के पैरामीटर मोटे दिखेंगे। यह निष्कर्ष निकालने का कारण देता है कि विद्युत क्षेत्र बस अनुपस्थित है। यदि अधिक सटीक सन्निकटन प्राप्त करना आवश्यक है, तो सिस्टम के सकारात्मक और नकारात्मक आरोपों के अलग-अलग समूहों को मानसिक रूप से एकत्रित करें, जिन पर विचार किया जा रहा है।
दूसरों के सापेक्ष उनके "केंद्रों" के विस्थापन के मामले में, ऐसी प्रणाली में क्षेत्र मापदंडों को एक ऐसे क्षेत्र के रूप में वर्णित किया जा सकता है जिसमें दो बिंदु आवेश होते हैं, परिमाण में बराबर और संकेत में विपरीत। यह ध्यान दिया जाता है कि वे दूसरों के संबंध में विस्थापित हैं। उपलब्ध करानाइस सन्निकटन के मापदंडों के संदर्भ में आवेश प्रणाली के अधिक सटीक लक्षण वर्णन के लिए, विद्युत क्षेत्र में द्विध्रुवीय के गुणों का अध्ययन करना आवश्यक होगा।
शब्द का परिचय
आइए परिभाषा पर वापस आते हैं। एक विद्युत द्विध्रुव एक प्रणाली की परिभाषा है जिसमें दो बिंदु आवेश होते हैं। उनके समान आकार और विपरीत संकेत हैं। इसके अलावा, ऐसे संकेत अन्य संकेतों के सापेक्ष कम दूरी पर स्थित होते हैं।
आप उस प्रक्रिया की विशेषता की गणना कर सकते हैं जो एक द्विध्रुवीय के माध्यम से बनाई गई है, और इसे दो बिंदु आवेशों द्वारा दर्शाया गया है: +q और −q, और वे दूसरों के सापेक्ष दूरी पर स्थित हैं।

गणना का क्रम
आइए द्विध्रुवीय की अक्षीय सतह पर क्षमता और तीव्रता की गणना करके शुरू करते हैं। यह एक सीधी रेखा है जो दो आवेशों के बीच चलती है। बशर्ते कि बिंदु A ऐसी दूरी पर स्थित हो जो द्विध्रुव के मध्य भाग के सापेक्ष r के बराबर हो, और यदि यह r >> a है, तो इस बिंदु पर क्षेत्र क्षमता के लिए सुपरपोजिशन के सिद्धांत के अनुसार, यह तर्कसंगत होगा विद्युत द्विध्रुव के प्राचलों की गणना करने के लिए व्यंजक का उपयोग करें।
शक्ति वेक्टर के परिमाण की गणना सुपरपोजिशन के सिद्धांत द्वारा की जाती है।क्षेत्र की ताकत की गणना करने के लिए, संभावित और क्षेत्र की ताकत के अनुपात की अवधारणा का उपयोग किया जाता है:
ईx=−Δφ /Δx.
ऐसी स्थितियों में, तीव्रता वेक्टर की दिशा द्विध्रुवीय अक्ष के सापेक्ष अनुदैर्ध्य रूप से इंगित की जाती है। इसके मापांक की गणना करने के लिए, मानक सूत्र लागू होता है।
महत्वपूर्णस्पष्टीकरण
यह ध्यान में रखा जाना चाहिए कि विद्युत द्विध्रुवीय क्षेत्र का कमजोर होना एक बिंदु आवेश का अनुभव करने की तुलना में तेजी से होता है। द्विध्रुवीय क्षेत्र की क्षमता का क्षय दूरी के वर्ग के व्युत्क्रमानुपाती होता है, और क्षेत्र की ताकत दूरी के घन के व्युत्क्रमानुपाती होती है।
समान, लेकिन अधिक बोझिल तरीकों का उपयोग करते हुए, द्विध्रुवीय की क्षमता और क्षेत्र की ताकत के मापदंडों को मनमाने बिंदुओं पर पाया जाता है, जिनमें से स्थिति मापदंडों को ध्रुवीय निर्देशांक के रूप में इस तरह की गणना पद्धति का उपयोग करके निर्धारित किया जाता है: की दूरी विद्युत द्विध्रुव का केंद्र (r) और कोण ().
तनाव वेक्टर का उपयोग करके गणना
तीव्रता वेक्टर ई की अवधारणा को दो बिंदुओं में बांटा गया है:
- रेडियल (Er), जो सीधी रेखा के सापेक्ष अनुदैर्ध्य दिशा में निर्देशित है।
- ऐसी एक सीधी रेखा निर्दिष्ट बिंदु और द्विध्रुव के केंद्र को उसके लंबवत के साथ जोड़ती है Eθ।
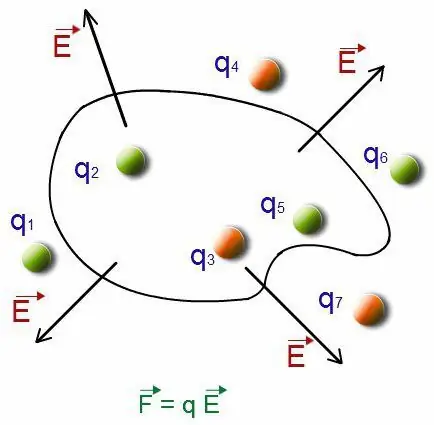
प्रत्येक घटक का यह अपघटन उस परिवर्तन के क्रम में निर्देशित होता है जो देखे जाने वाले बिंदु के सभी निर्देशांकों के साथ होता है। आप इसे उस अनुपात से पा सकते हैं जो संभावित संशोधनों के लिए क्षेत्र शक्ति संकेतकों से संबंधित है।
क्षेत्र की ताकत पर वेक्टर घटक का पता लगाना, वैक्टर की दिशा में अवलोकन बिंदु के विस्थापन के कारण होने वाले संभावित परिवर्तनों में संबंध की प्रकृति को स्थापित करना महत्वपूर्ण है।
लंबवत घटक की गणना करें
जब हो गयाइस प्रक्रिया के लिए, यह ध्यान रखना महत्वपूर्ण है कि एक छोटे लंबवत विस्थापन पर परिमाण के लिए व्यंजक कोण को बदलकर निर्धारित किया जाएगा: l=rΔθ.इस क्षेत्र घटक के लिए परिमाण पैरामीटर बराबर होंगे।
अनुपात प्राप्त करने के बाद, इस क्षेत्र के बल की रेखाओं के साथ एक चित्र बनाने के लिए एक मनमाना बिंदु पर विद्युत द्विध्रुव का क्षेत्र निर्धारित करना संभव है।
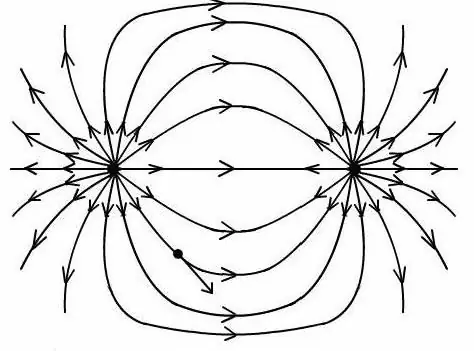
यह विचार करना महत्वपूर्ण है कि एक द्विध्रुवीय की क्षमता और क्षेत्र की ताकत का निर्धारण करने के लिए सभी सूत्र केवल उन मूल्यों के उत्पाद पर काम करते हैं जो एक द्विध्रुवीय आवेश में होते हैं और उनके बीच की दूरी होती है।
द्विध्रुवीय क्षण
वर्णित कार्य का शीर्षक विद्युत प्रकार के गुणों का पूर्ण विवरण है। इसका नाम "सिस्टम का द्विध्रुवीय क्षण" है।
एक द्विध्रुव की परिभाषा से, जो बिंदु आवेशों की एक प्रणाली है, यह पता लगाया जा सकता है कि यह अक्षीय समरूपता की उपस्थिति की विशेषता है, जब अक्ष एक सीधी रेखा है जो कई आवेशों से होकर गुजरती है।
द्विध्रुव के पूर्ण अभिलक्षण को सेट करने के लिए, अक्ष की ओरिएंटेशन दिशा इंगित करें। गणना की सादगी के लिए, द्विध्रुवीय क्षण वेक्टर निर्दिष्ट किया जा सकता है। इसके परिमाण का मान द्विध्रुवीय क्षण के परिमाण के बराबर होता है, और दिशा वेक्टर इसके संयोग और द्विध्रुव की धुरी से भिन्न होता है। तो, p=qa यदि a उस सदिश की दिशा है जो द्विध्रुव के ऋणात्मक और धनात्मक आवेशों को जोड़ता है।
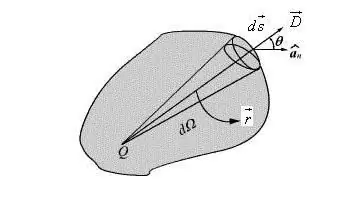
द्विध्रुव की ऐसी विशेषता का उपयोग सुविधाजनक है और ज्यादातर मामलों में सूत्र को सरल बनाना और इसे रूप देना संभव बनाता हैवेक्टर। एक मनमाना दिशा के एक बिंदु पर द्विध्रुवीय क्षेत्र की क्षमता का विवरण एक वेक्टर के रूप में लिखा जाता है।
एक द्विध्रुवीय की वेक्टर विशेषता और उसके द्विध्रुवीय क्षण के रूप में ऐसी अवधारणाओं की शुरूआत एक सरल मॉडल का उपयोग करके की जा सकती है - एक समान क्षेत्र में एक बिंदु आवेश, जिसमें आवेशों की एक प्रणाली शामिल होती है, जिसके ज्यामितीय आयाम होते हैं ध्यान में नहीं रखा जाना चाहिए, लेकिन द्विध्रुवीय क्षण को जानना महत्वपूर्ण है। गणना करने के लिए यह एक पूर्वापेक्षा है।
द्विध्रुव कैसे व्यवहार करता है
द्विध्रुव का व्यवहार ऐसी स्थिति के उदाहरण पर देखा जा सकता है। दो बिंदु आवेशों की स्थिति में एक दूसरे के सापेक्ष दूरी का एक निश्चित चरित्र होता है। उन्हें एक समान विद्युत क्षेत्र के द्विध्रुव की स्थितियों में रखा गया था। प्रक्रिया का अवलोकन किया। भौतिकी (इलेक्ट्रोडायनामिक्स) के पाठों में इस अवधारणा पर विस्तार से विचार किया गया है। क्षेत्र से आवेश तक बलों की क्रिया की जाती है:
एफ=±क्यूई
ये परिमाण में बराबर और दिशा में विपरीत होते हैं। द्विध्रुव पर कार्य करने वाले कुल बल का सूचक शून्य होता है। चूँकि इस तरह के बल का विभिन्न बिंदुओं पर प्रभाव पड़ता है, कुल क्षण होगा:
एम=फा पाप ए=क्यूई पाप ए=पीई पाप ए
साथ में α क्षेत्र शक्ति वैक्टर और द्विध्रुवीय क्षण वैक्टर को जोड़ने वाला कोण है। बल आघूर्ण की उपस्थिति के कारण, निकाय का द्विध्रुव आघूर्ण विद्युत क्षेत्र शक्ति सदिश की दिशा में लौट जाता है।
विद्युत द्विध्रुव एक अवधारणा है जिसे स्पष्ट रूप से समझना महत्वपूर्ण है। आप इसके बारे में इंटरनेट पर अधिक पढ़ सकते हैं। यह भी कर सकते हैंजैसा कि हमने ऊपर बात की, कक्षा 10 में स्कूल में भौतिकी के पाठों में अध्ययन करने के लिए।






