समानांतर और सीरियल कनेक्शन। कंडक्टरों की श्रृंखला और समानांतर कनेक्शन

2024 लेखक: Angel Austin | [email protected]. अंतिम बार संशोधित: 2024-01-02 17:47

भौतिकी में, समानांतर और श्रृंखला कनेक्शन के विषय का अध्ययन किया जाता है, और यह न केवल कंडक्टर हो सकता है, बल्कि कैपेसिटर भी हो सकता है। यहां यह महत्वपूर्ण है कि इस बारे में भ्रमित न हों कि उनमें से प्रत्येक आरेख पर कैसा दिखता है। और उसके बाद ही विशिष्ट सूत्र लागू करें। वैसे तो आपको उन्हें दिल से याद करने की जरूरत है।

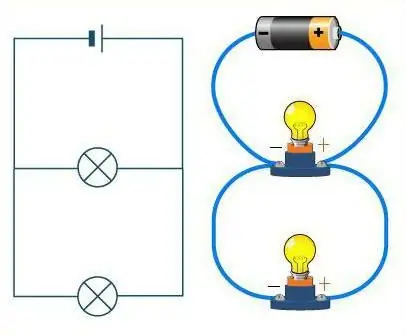
इन दो यौगिकों में अंतर कैसे करें?

आरेख पर करीब से नज़र डालें। यदि तारों को सड़क के रूप में दर्शाया जाता है, तो उस पर चलने वाली कारें प्रतिरोधों की भूमिका निभाएंगी। बिना कांटे के सीधी सड़क पर, कारें एक के बाद एक, एक श्रृंखला में चलती हैं। कंडक्टरों का श्रृंखला कनेक्शन भी समान दिखता है। इस मामले में सड़क में असीमित संख्या में मोड़ हो सकते हैं, लेकिन एक भी चौराहा नहीं। कोई फर्क नहीं पड़ता कि सड़क (तारों) कैसे लड़खड़ाती है, मशीनें (प्रतिरोधक) हमेशा एक के बाद एक, एक श्रृंखला में स्थित होंगी।

एक समानांतर कनेक्शन पर विचार किया जाए तो यह काफी अलग बात है। फिर प्रतिरोधों की तुलना शुरुआत में एथलीटों से की जा सकती है। वो हैंप्रत्येक अपने स्वयं के ट्रैक पर खड़ा होता है, लेकिन उनकी गति की दिशा समान होती है, और फिनिश लाइन एक ही स्थान पर होती है। इसी तरह, प्रतिरोधक - उनमें से प्रत्येक का अपना तार होता है, लेकिन वे सभी किसी न किसी बिंदु पर जुड़े होते हैं।

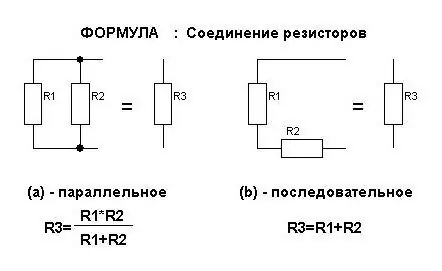
वर्तमान ताकत के लिए सूत्र

इसकी चर्चा हमेशा "बिजली" विषय में होती है। समानांतर और श्रृंखला कनेक्शन विभिन्न तरीकों से प्रतिरोधों में करंट की मात्रा को प्रभावित करते हैं। उनके लिए ऐसे सूत्र व्युत्पन्न होते हैं जिन्हें याद किया जा सकता है। लेकिन यह केवल उस अर्थ को याद रखने के लिए पर्याप्त है जो उनमें निवेश किया गया है।

इसलिए, कंडक्टरों के श्रृंखला कनेक्शन में वर्तमान हमेशा समान होता है। यानी उनमें से प्रत्येक में वर्तमान ताकत का मूल्य अलग नहीं है। यदि आप तार की तुलना पाइप से करते हैं तो आप एक सादृश्य बना सकते हैं। इसमें हमेशा इसी तरह पानी बहता रहता है। और उसके मार्ग की सभी बाधाएं उसी बल से दूर हो जाएंगी। वर्तमान के साथ ही। इसलिए, प्रतिरोधों के एक श्रृंखला कनेक्शन के साथ एक सर्किट में कुल करंट का सूत्र इस तरह दिखता है:

मैं _जीन=मैं ₁=मैं ₂

यहाँ I अक्षर करंट की ताकत को दर्शाता है। यह एक सामान्य संकेतन है, इसलिए आपको इसे याद रखने की आवश्यकता है।

समानांतर कनेक्शन में करंट अब स्थिर मान नहीं रहेगा। एक पाइप के समान समानता के साथ, यह पता चला है कि यदि मुख्य पाइप में एक शाखा है तो पानी दो धाराओं में विभाजित हो जाएगा। यही घटना करंट के साथ तब देखी जाती है जब इसके रास्ते में तारों की एक शाखा दिखाई देती है। कंडक्टरों को समानांतर में जोड़ने पर कुल वर्तमान ताकत का सूत्र:

मैं _जीन=मैं ₁ + मैं ₂

अगर शाखा तारों से बनी हो तोदो से अधिक, तो उपरोक्त सूत्र में समान संख्या से अधिक पद होंगे।

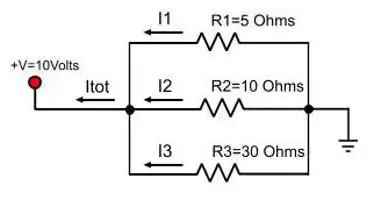
तनाव के लिए सूत्र

जब एक सर्किट माना जाता है जिसमें कंडक्टर श्रृंखला में जुड़े होते हैं, तो पूरे खंड में वोल्टेज प्रत्येक विशिष्ट प्रतिरोधी पर इन मानों के योग से निर्धारित होता है। आप इस स्थिति की तुलना प्लेटों से कर सकते हैं। एक व्यक्ति के लिए उनमें से एक को पकड़ना आसान होगा, वह दूसरे को भी पास में ले जा सकेगा, लेकिन कठिनाई से। एक व्यक्ति अब एक दूसरे के बगल में तीन प्लेट नहीं रख पाएगा, एक सेकंड की मदद की आवश्यकता होगी। आदि। लोगों के प्रयास जुड़ते हैं।

कंडक्टर के एक श्रृंखला कनेक्शन के साथ एक सर्किट के एक खंड के कुल वोल्टेज के लिए सूत्र इस तरह दिखता है:

U _gen=U ₁ + U _{2, जहां यू को अपनाया गया पदनाम है विद्युत वोल्टेज के लिए।}

प्रतिरोधों के समानांतर कनेक्शन पर विचार करने पर एक और स्थिति उत्पन्न होती है। जब प्लेटों को एक दूसरे के ऊपर रखा जाता है, तब भी वे एक व्यक्ति द्वारा पकड़ी जा सकती हैं। तो आपको कुछ भी जोड़ने की जरूरत नहीं है। जब कंडक्टर समानांतर में जुड़े होते हैं तो वही सादृश्य देखा जाता है। उनमें से प्रत्येक पर वोल्टेज समान और बराबर होता है जो उन सभी पर एक ही बार में होता है। कुल वोल्टेज का सूत्र है:

यू _जीन=यू ₁=यू ₂

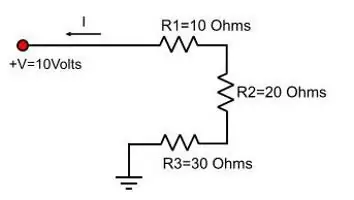
विद्युत प्रतिरोध के सूत्र

अब आप उन्हें याद नहीं कर सकते, लेकिन ओम के नियम के सूत्र को जान सकते हैं और उससे वांछित प्राप्त कर सकते हैं। इस कानून से यह निम्नानुसार है किवोल्टेज वर्तमान और प्रतिरोध के उत्पाद के बराबर है। अर्थात्, U=IR, जहाँ R प्रतिरोध है।

फिर आपको जिस फॉर्मूले के साथ काम करना होगा, वह इस बात पर निर्भर करता है कि कंडक्टर कैसे जुड़े हैं:

• श्रृंखला में, इसलिए आपको वोल्टेज के लिए समानता की आवश्यकता है - I_genR_total=I_{1 आर}1 _{+ मैं}2_आर2;
• समानांतर में, वर्तमान ताकत के लिए सूत्र का उपयोग करना आवश्यक है - यू_कुल / आर_कुल=यू 1_{/ आर}1 _{+ यू}2 _{/ आर}2 _।

सरल परिवर्तनों के बाद, जो इस तथ्य पर आधारित हैं कि पहली समानता में सभी धाराओं का मान समान है, और दूसरे में - वोल्टेज समान हैं। तो उन्हें छोटा किया जा सकता है। अर्थात् निम्नलिखित भाव प्राप्त होते हैं:

1. R _gen=R ₁ + R _{2 (कंडक्टरों के सीरीज कनेक्शन के लिए)}
2. 1 / आर _जीन=1 / आर ₁ + 1 / आर _{2(समानांतर में जुड़े होने पर)।}

जब नेटवर्क से जुड़े प्रतिरोधकों की संख्या बढ़ती है, तो इन भावों में पदों की संख्या बदल जाती है।

यह ध्यान देने योग्य है कि कंडक्टरों के समानांतर और श्रृंखला कनेक्शन का कुल प्रतिरोध पर एक अलग प्रभाव पड़ता है। उनमें से पहला सर्किट सेक्शन के प्रतिरोध को कम करता है। इसके अलावा, यह इस्तेमाल किए गए प्रतिरोधों में से सबसे छोटे से कम निकला। श्रृंखला में जुड़े होने पर, सब कुछ तार्किक होता है: मान जुड़ जाते हैं, इसलिए कुल संख्या हमेशा सबसे बड़ी होगी।

वर्तमान कार्य

पिछली तीन मात्राएं एक सर्किट में कंडक्टरों के समानांतर कनेक्शन और श्रृंखला व्यवस्था के नियम बनाती हैं। इसलिए उन्हें जानना जरूरी है। काम और शक्ति के बारे में, आपको बस मूल सूत्र याद रखने की जरूरत है। यह इस प्रकार लिखा गया है: ए \u003d आईयूटी, जहां ए वर्तमान का काम है, टी कंडक्टर के माध्यम से इसके पारित होने का समय है।

सीरियल कनेक्शन के साथ कुल कार्य निर्धारित करने के लिए, आपको मूल अभिव्यक्ति में वोल्टेज को बदलने की आवश्यकता है। आपको समानता मिलती है: A \u003d I(U ₁ + U _{2)t, कोष्ठक खोलना जिसमें यह पता चलता है कि पूरे खंड पर काम उनके लिए प्रत्येक विशिष्ट वर्तमान उपभोक्ता पर राशि के बराबर है।}

यदि समानांतर कनेक्शन योजना पर विचार किया जाता है तो तर्क समान रूप से आगे बढ़ता है। केवल वर्तमान ताकत को बदला जाना चाहिए। लेकिन परिणाम वही होगा: ए=ए ₁ + ए _2।

वर्तमान शक्ति

सर्किट सेक्शन के पावर (नोटेशन "पी") के लिए फॉर्मूला प्राप्त करते समय, आपको फिर से एक फॉर्मूला का उपयोग करने की आवश्यकता होती है: पी \u003d यूआई। इस तरह के तर्क के बाद, यह पता चलता है कि समानांतर और श्रृंखला कनेक्शन हैं शक्ति के लिए इस तरह के सूत्र द्वारा वर्णित: पी \u003d पी1 _{+ पी} 2_।

अर्थात् योजनाएँ कैसी भी हों, कार्य में लगे लोगों का योग ही कुल शक्ति होगी। यह इस तथ्य की व्याख्या करता है कि एक ही समय में अपार्टमेंट नेटवर्क में कई शक्तिशाली उपकरणों को शामिल करना असंभव है। वह बस भार नहीं उठा सकती।

नए साल की माला की मरम्मत कंडक्टरों के कनेक्शन को कैसे प्रभावित करती है?

एक बल्ब के जलने के तुरंत बाद, यह स्पष्ट हो जाता है कि वे कैसे जुड़े थे। परसीरियल कनेक्शन, उनमें से कोई भी प्रकाश नहीं करेगा। यह इस तथ्य के कारण है कि एक दीपक जो अनुपयोगी हो गया है, सर्किट में एक ब्रेक बनाता है। इसलिए, आपको यह निर्धारित करने के लिए सब कुछ जांचना होगा कि कौन सा जल गया है, इसे बदलें - और माला काम करना शुरू कर देगी।

यदि यह एक समानांतर कनेक्शन का उपयोग करता है, तो यह काम करना बंद नहीं करता है यदि एक बल्ब विफल हो जाता है। आखिरकार, श्रृंखला पूरी तरह से नहीं टूटेगी, लेकिन केवल एक समानांतर हिस्सा होगा। ऐसी माला की मरम्मत के लिए, आपको सर्किट के सभी तत्वों की जांच करने की आवश्यकता नहीं है, लेकिन केवल वे जो चमकते नहीं हैं।

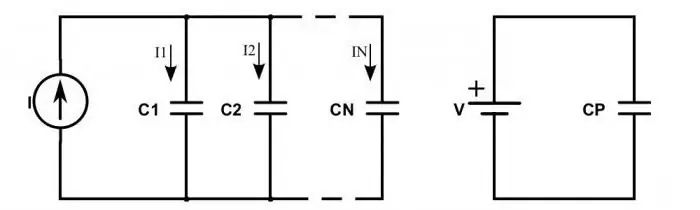
यदि प्रतिरोधों के स्थान पर संधारित्रों को शामिल किया जाए तो परिपथ का क्या होता है?

जब वे श्रृंखला में जुड़े होते हैं, तो निम्न स्थिति देखी जाती है: शक्ति स्रोत के प्लस से चार्ज केवल चरम कैपेसिटर की बाहरी प्लेटों पर आते हैं। बीच में बस उस चार्ज को चेन के साथ पास करते हैं। यह इस तथ्य की व्याख्या करता है कि सभी प्लेटों पर समान आवेश दिखाई देते हैं, लेकिन विभिन्न संकेतों के साथ। इसलिए, श्रृंखला में जुड़े प्रत्येक संधारित्र का विद्युत आवेश इस प्रकार लिखा जा सकता है:

क्यू _जीन =क्यू ₁=क्यू _2।

प्रत्येक संधारित्र पर वोल्टेज निर्धारित करने के लिए, आपको सूत्र जानने की आवश्यकता होगी: यू=क्यू / सी। इसमें, सी संधारित्र की समाई है।

कुल वोल्टेज प्रतिरोधों के समान नियम का पालन करता है। इसलिए, समाई सूत्र में वोल्टेज को योग के साथ बदलकर, हम पाते हैं कि उपकरणों की कुल समाई की गणना सूत्र का उपयोग करके की जानी चाहिए:

सी=क्यू / (यू ₁ + यू_2).

आप फ्रैक्शंस को फ्लिप करके और वोल्टेज के अनुपात को कैपेसिटेंस के साथ चार्ज करके इस फॉर्मूले को सरल बना सकते हैं। यह निम्नलिखित समानता प्राप्त करता है: 1 /=1 / ₁ + 1 / С _2।

जब कैपेसिटर समानांतर में जुड़े होते हैं तो स्थिति कुछ अलग दिखती है। फिर कुल शुल्क सभी उपकरणों की प्लेटों पर जमा होने वाले सभी शुल्कों के योग से निर्धारित होता है। और वोल्टेज मान अभी भी सामान्य कानूनों के अनुसार निर्धारित किया जाता है। इसलिए, समानांतर में जुड़े कैपेसिटर की कुल समाई का सूत्र है:

С=(क्यू 1 + क्यू 2) / यू.

अर्थात, इस मान को कनेक्शन में उपयोग किए जाने वाले प्रत्येक डिवाइस के योग के रूप में माना जाता है:

एस=एस ₁ + एस _2.

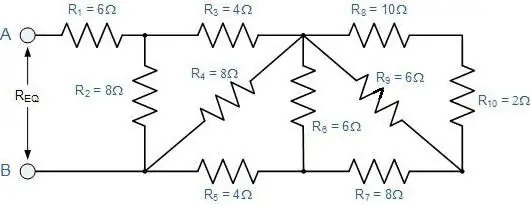
कंडक्टरों के एक मनमाना कनेक्शन के कुल प्रतिरोध का निर्धारण कैसे करें?

अर्थात, एक जिसमें क्रमिक खंड समानांतर वाले को प्रतिस्थापित करते हैं, और इसके विपरीत। उनके लिए, वर्णित सभी कानून अभी भी मान्य हैं। केवल आपको उन्हें चरणों में लागू करने की आवश्यकता है।

सबसे पहले, यह योजना का मानसिक रूप से विस्तार करने वाला है। यदि इसकी कल्पना करना कठिन है, तो आपको यह आकर्षित करने की आवश्यकता है कि क्या होता है। स्पष्टीकरण स्पष्ट हो जाएगा यदि हम इसे एक विशिष्ट उदाहरण के साथ मानते हैं (आंकड़ा देखें)।

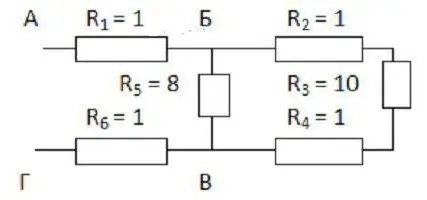
बिन्दु बी और सी से ड्राइंग शुरू करना सुविधाजनक है। उन्हें एक दूसरे से और शीट के किनारों से कुछ दूरी पर रखा जाना चाहिए। बाईं ओर, एक तार बिंदु B तक पहुंचता है, और दो पहले से ही दाईं ओर निर्देशित होते हैं। दूसरी ओर, बिंदु B की बाईं ओर दो शाखाएँ हैं, और उसके बाद एक तार है।

अब आपको इनके बीच खाली जगह भरने की जरूरत हैबिंदु 2, 3 और 4 के गुणांक वाले तीन प्रतिरोधों को शीर्ष तार के साथ रखा जाना चाहिए, और 5 के सूचकांक वाला एक नीचे से जाएगा। पहले तीन श्रृंखला में जुड़े हुए हैं। पांचवें रोकनेवाला के साथ वे समानांतर में हैं।

शेष दो प्रतिरोधक (पहला और छठा) बीवी के माने गए खंड के साथ श्रृंखला में जुड़े हुए हैं। इसलिए, ड्राइंग को केवल चयनित बिंदुओं के दोनों ओर दो आयतों के साथ पूरक किया जा सकता है। प्रतिरोध की गणना के लिए सूत्रों को लागू करना बाकी है:

• पहले वाला जो सीरियल कनेक्शन के लिए दिया गया था;
• फिर समानांतर के लिए;
• और फिर लगातार।

इस तरह, आप किसी भी बहुत जटिल योजना को लागू कर सकते हैं।

कंडक्टरों के सीरियल कनेक्शन की समस्या

हालत। दो लैंप और एक रोकनेवाला एक दूसरे के पीछे एक सर्किट में जुड़े हुए हैं। कुल वोल्टेज 110 वी है और करंट 12 ए है। यदि प्रत्येक लैंप को 40 वी पर रेट किया गया है तो रोकनेवाला का मूल्य क्या है?

निर्णय। चूंकि एक श्रृंखला कनेक्शन पर विचार किया जा रहा है, इसके कानूनों के सूत्र ज्ञात हैं। आपको बस उन्हें सही तरीके से लागू करने की जरूरत है। रोकनेवाला भर में वोल्टेज मान का पता लगाकर शुरू करें। ऐसा करने के लिए, आपको कुल से एक दीपक के वोल्टेज का दो गुना घटाना होगा। यह 30 वी निकला।

अब जबकि दो मात्राएँ ज्ञात हैं, U और I (उनमें से दूसरी स्थिति में दी गई है, क्योंकि कुल धारा प्रत्येक श्रृंखला के उपभोक्ता में करंट के बराबर है), हम इसका उपयोग करके रोकनेवाला के प्रतिरोध की गणना कर सकते हैं ओम कानून। यह 2.5 ओम निकला।

जवाब। रोकनेवाला का प्रतिरोध 2.5 ओम है।

कार्यकैपेसिटर, समानांतर और श्रृंखला के कनेक्शन के लिए

हालत। 20, 25 और 30 माइक्रोफ़ारड की क्षमता वाले तीन कैपेसिटर हैं। श्रृंखला और समानांतर में जुड़े होने पर उनकी कुल समाई निर्धारित करें।

निर्णय। समानांतर कनेक्शन से शुरू करना आसान है। इस स्थिति में, केवल तीनों मानों को जोड़ने की आवश्यकता है। इस प्रकार, कुल धारिता 75uF है।

जब ये कैपेसिटर श्रृंखला में जुड़े होते हैं तो गणना कुछ अधिक जटिल हो जाएगी। आखिरकार, पहले आपको इनमें से प्रत्येक क्षमता में एकता का अनुपात खोजने की जरूरत है, और फिर उन्हें एक-दूसरे से जोड़ना होगा। यह पता चला है कि कुल क्षमता से विभाजित इकाई 37/300 है। तब वांछित मान लगभग 8 माइक्रोफ़ारड है।

जवाब। श्रृंखला कनेक्शन में कुल समाई 8 uF है, समानांतर में - 75 uF।