हमारे आस-पास की प्राकृतिक घटनाएं और प्रक्रियाएं काफी जटिल हैं। उनके सटीक भौतिक विवरण के लिए, एक बोझिल गणितीय उपकरण का उपयोग किया जाना चाहिए और बड़ी संख्या में महत्वपूर्ण कारकों को ध्यान में रखा जाना चाहिए। इस समस्या से बचने के लिए, भौतिकी में कुछ सरलीकृत मॉडल का उपयोग किया जाता है, जो प्रक्रिया के गणितीय विश्लेषण की सुविधा प्रदान करते हैं, लेकिन व्यावहारिक रूप से इसके विवरण की सटीकता को प्रभावित नहीं करते हैं। उनमें से एक आदर्श गैस मॉडल है। आइए लेख में इस पर अधिक विस्तार से विचार करें।
आदर्श गैस की अवधारणा
एक आदर्श गैस एक पदार्थ के एकत्रीकरण की स्थिति है, जिसमें भौतिक बिंदु होते हैं जो एक दूसरे के साथ बातचीत नहीं करते हैं। आइए इस परिभाषा को और विस्तार से समझाते हैं।
सबसे पहले, हम भौतिक बिंदुओं के बारे में उन वस्तुओं के रूप में बात कर रहे हैं जो एक आदर्श गैस बनाती हैं। इसका मतलब है कि इसके अणुओं और परमाणुओं का आकार नहीं होता है, लेकिन एक निश्चित द्रव्यमान होता है। यह बोल्ड हैइस तथ्य को ध्यान में रखते हुए एक अनुमान लगाया जा सकता है कि कम दबाव और उच्च तापमान पर सभी वास्तविक गैसों में अणुओं के बीच की दूरी उनके रैखिक आयामों से बहुत अधिक होती है।
दूसरे, आदर्श गैस के अणुओं को आपस में परस्पर क्रिया नहीं करनी चाहिए। वास्तव में, ऐसी बातचीत हमेशा मौजूद रहती है। तो, महान गैसों के परमाणु भी द्विध्रुव-द्विध्रुवीय आकर्षण का अनुभव करते हैं। दूसरे शब्दों में, वैन डेर वाल्स इंटरैक्शन मौजूद हैं। हालांकि, घूर्णन की गतिज ऊर्जा और अणुओं के स्थानांतरीय गति की तुलना में, ये अंतःक्रियाएं इतनी छोटी हैं कि वे गैसों के गुणों को प्रभावित नहीं करती हैं। इसलिए, व्यावहारिक समस्याओं को हल करते समय उन पर विचार नहीं किया जा सकता है।
यह ध्यान रखना महत्वपूर्ण है कि सभी गैसें जिनमें घनत्व कम है और तापमान अधिक है, उन्हें आदर्श नहीं माना जा सकता है। वैन डेर वाल्स इंटरैक्शन के अलावा, अन्य, मजबूत प्रकार के बॉन्ड हैं, उदाहरण के लिए, एच 2O अणुओं के बीच हाइड्रोजन बॉन्ड, जो गैस आदर्शता की स्थिति का घोर उल्लंघन करते हैं। इस कारण जलवाष्प एक आदर्श गैस नहीं है, बल्कि वायु है।
आदर्श गैस का भौतिक मॉडल
इस मॉडल को निम्नानुसार दर्शाया जा सकता है: मान लीजिए कि गैस प्रणाली में एन कण होते हैं। ये विभिन्न रसायनों और तत्वों के परमाणु और अणु हो सकते हैं। एन कणों की संख्या बड़ी है, इसलिए आमतौर पर इसका वर्णन करने के लिए इकाई "मोल" का उपयोग किया जाता है (1 तिल एवोगैड्रो की संख्या से मेल खाता है)। ये सभी किसी न किसी आयतन V में गति करते हैं। कण गतिअराजक और एक दूसरे से स्वतंत्र हैं। उनमें से प्रत्येक की एक निश्चित गति v है और वह एक सीधे रास्ते पर चलता है।
सैद्धांतिक रूप से, कणों के बीच टकराव की संभावना लगभग शून्य है, क्योंकि उनका आकार इंटरपार्टिकल दूरी की तुलना में छोटा है। हालांकि, अगर ऐसी टक्कर होती है, तो यह बिल्कुल लोचदार है। बाद के मामले में, कणों का कुल संवेग और उनकी गतिज ऊर्जा संरक्षित रहती है।
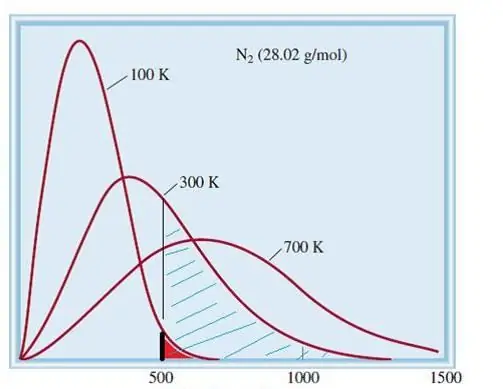
आदर्श गैसों का माना मॉडल एक शास्त्रीय प्रणाली है जिसमें बड़ी संख्या में तत्व होते हैं। इसलिए, इसमें कणों की गति और ऊर्जा मैक्सवेल-बोल्ट्जमैन के सांख्यिकीय वितरण का पालन करती है। कुछ कणों का वेग कम होता है, जबकि अन्य में उच्च वेग होता है। इस मामले में, एक निश्चित संकीर्ण गति सीमा है, जिसमें इस मात्रा के सबसे संभावित मूल्य निहित हैं। नाइट्रोजन अणुओं का वेग वितरण नीचे योजनाबद्ध रूप से दिखाया गया है।
गैसों का गतिज सिद्धांत
ऊपर वर्णित आदर्श गैसों का मॉडल विशिष्ट रूप से गैसों के गुणों को निर्धारित करता है। यह मॉडल पहली बार 1738 में डेनियल बर्नौली द्वारा प्रस्तावित किया गया था।

बाद में, इसे अगस्त क्रोनिग, रुडोल्फ क्लॉसियस, मिखाइल लोमोनोसोव, जेम्स मैक्सवेल, लुडविग बोल्ट्ज़मैन, मैरियन स्मोलुचोव्स्की और अन्य वैज्ञानिकों द्वारा अपनी वर्तमान स्थिति में विकसित किया गया था।
द्रव पदार्थों का गतिज सिद्धांत, जिसके आधार पर आदर्श गैस मॉडल बनाया गया है, इसके सूक्ष्म व्यवहार के आधार पर प्रणाली के दो महत्वपूर्ण मैक्रोस्कोपिक गुणों की व्याख्या करता है:
- गैसों में दबाव बर्तन की दीवारों के साथ कणों के टकराने का परिणाम है।
- सिस्टम में तापमान अणुओं और परमाणुओं की निरंतर गति के प्रकट होने का परिणाम है।
आइए गतिज सिद्धांत के दोनों निष्कर्षों पर विस्तार करें।
गैस का दबाव
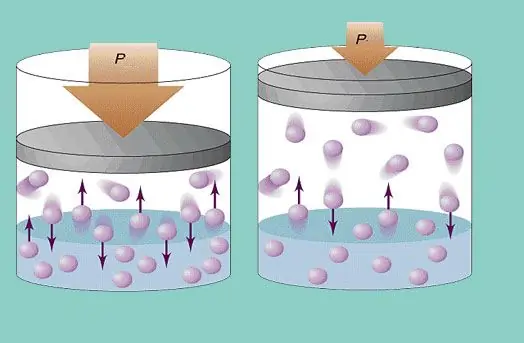
आदर्श गैस मॉडल प्रणाली में कणों की निरंतर अराजक गति और पोत की दीवारों के साथ उनके निरंतर टकराव को मानता है। इस तरह के प्रत्येक टकराव को बिल्कुल लोचदार माना जाता है। कण द्रव्यमान छोटा है (≈10-27-10-25 किलो)। इसलिए, यह टक्कर में बहुत अधिक दबाव नहीं बना सकता है। फिर भी, कणों की संख्या, और इसलिए टक्करों की संख्या बहुत बड़ी है (≈1023)। इसके अलावा, कमरे के तापमान पर तत्वों का मूल माध्य वर्ग वेग कई सौ मीटर प्रति सेकंड है। यह सब पोत की दीवारों पर काफी दबाव पैदा करता है। इसकी गणना निम्न सूत्र का उपयोग करके की जा सकती है:
पी=एनएमवीसीपी2 / (3वी), जहाँ vcp मूल माध्य वर्ग वेग है, m कण द्रव्यमान है।
पूर्ण तापमान
आदर्श गैस मॉडल के अनुसार, तापमान विशिष्ट रूप से अध्ययन के तहत सिस्टम में एक अणु या परमाणु की औसत गतिज ऊर्जा से निर्धारित होता है। आप निम्न व्यंजक लिख सकते हैं जो एक आदर्श गैस के लिए गतिज ऊर्जा और निरपेक्ष तापमान से संबंधित है:
मवीसीपी2 /2=3/2केबी टी.
यहाँ kB बोल्ट्ज़मान नियतांक है। इस समानता से हमें प्राप्त होता है:
टी=एम vcp2 / (3kB)।
राज्य का सार्वभौमिक समीकरण
यदि हम उपरोक्त भावों को पूर्ण दबाव P और पूर्ण तापमान T के लिए जोड़ते हैं, तो हम निम्नलिखित समानता लिख सकते हैं:
पीवी=एनआरटी.
यहाँ n मोल्स में पदार्थ की मात्रा है, R गैस स्थिरांक है जो D. I. मेंडेलीव द्वारा पेश किया गया है। आदर्श गैसों के सिद्धांत में यह अभिव्यक्ति सबसे महत्वपूर्ण समीकरण है, क्योंकि यह तीन थर्मोडायनामिक मापदंडों (वी, पी, टी) को जोड़ती है और गैस प्रणाली की रासायनिक विशेषताओं पर निर्भर नहीं करती है।

सार्वभौम समीकरण पहले 19वीं शताब्दी में फ्रांसीसी भौतिक विज्ञानी एमिल क्लैपेरॉन द्वारा प्रयोगात्मक रूप से प्राप्त किया गया था और फिर रूसी रसायनज्ञ मेंडेलीव द्वारा अपने आधुनिक रूप में लाया गया था, यही कारण है कि वर्तमान में इन वैज्ञानिकों के नाम हैं।






