एमसीटी मूल समीकरण और तापमान माप

2024 लेखक: Angel Austin | [email protected]. अंतिम बार संशोधित: 2024-01-15 17:24

सांख्यिकीय प्रणालियों में होने वाली प्रक्रियाओं का अध्ययन कणों के न्यूनतम आकार और उनकी विशाल संख्या से जटिल है। प्रत्येक कण पर अलग से विचार करना व्यावहारिक रूप से असंभव है, इसलिए, सांख्यिकीय मात्रा पेश की जाती है: कणों की औसत गति, उनकी एकाग्रता, कण द्रव्यमान। सूक्ष्म मापदंडों को ध्यान में रखते हुए प्रणाली की स्थिति को दर्शाने वाले सूत्र को गैसों के आणविक-गतिज सिद्धांत (MKT) का मूल समीकरण कहा जाता है।

कणों की औसत गति के बारे में थोड़ा सा

कणों की गति का निर्धारण सबसे पहले प्रयोगात्मक रूप से किया गया था। ओटो स्टर्न द्वारा संचालित स्कूल पाठ्यक्रम के एक प्रसिद्ध प्रयोग ने कण वेगों का एक विचार बनाना संभव बना दिया। प्रयोग के दौरान, घूर्णन सिलेंडरों में चांदी के परमाणुओं की गति का अध्ययन किया गया था: पहले, स्थापना की स्थिर अवस्था में, फिर जब यह एक निश्चित कोणीय वेग के साथ घूमता था।

परिणामस्वरूप, यह पाया गया कि चांदी के अणुओं की गति ध्वनि की गति से अधिक है और 500 मीटर/सेकेंड है। तथ्य काफी दिलचस्प है, क्योंकि किसी व्यक्ति के लिए पदार्थों में कणों की गति की ऐसी गति को महसूस करना मुश्किल है।

आदर्श गैस

अनुसंधान जारी रखेंयह केवल उस प्रणाली में संभव लगता है जिसके मापदंडों को भौतिक उपकरणों का उपयोग करके प्रत्यक्ष माप द्वारा निर्धारित किया जा सकता है। स्पीड को स्पीडोमीटर से मापा जाता है, लेकिन स्पीडोमीटर को एक कण से जोड़ने का विचार बेतुका है। कण गति से जुड़े केवल एक मैक्रोस्कोपिक पैरामीटर को सीधे मापा जा सकता है।

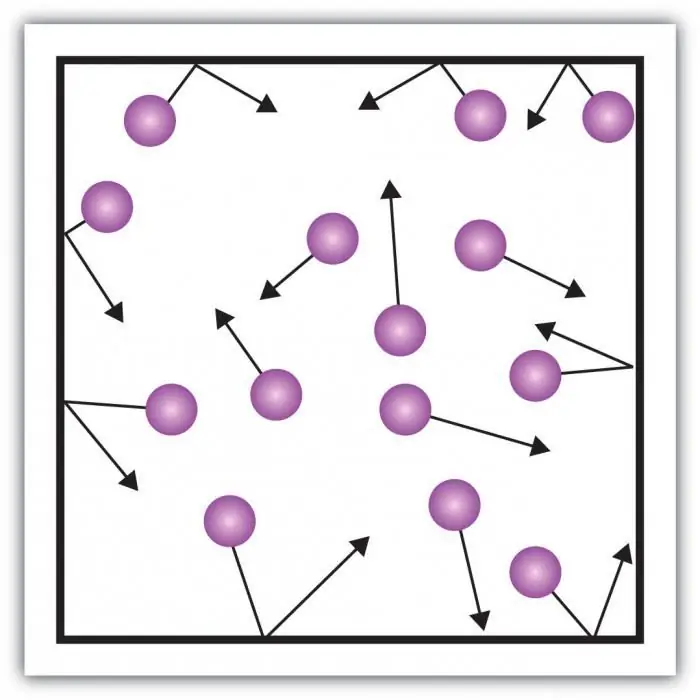
गैस के दबाव पर विचार करें। बर्तन में गैस के अणुओं के प्रभाव से बर्तन की दीवारों पर दबाव बनता है। पदार्थ की गैसीय अवस्था की ख़ासियत कणों के बीच पर्याप्त बड़ी दूरी और एक दूसरे के साथ उनकी छोटी बातचीत है। यह आपको इसके दबाव को सीधे मापने की अनुमति देता है।

परस्पर क्रिया करने वाले पिंडों की कोई भी प्रणाली संभावित ऊर्जा और गति की गतिज ऊर्जा की विशेषता है। वास्तविक गैस एक जटिल प्रणाली है। स्थितिज ऊर्जा की परिवर्तनशीलता स्वयं को व्यवस्थित करने के लिए उधार नहीं देती है। समस्या को एक मॉडल पेश करके हल किया जा सकता है जो बातचीत की जटिलता को दूर करते हुए गैस के विशिष्ट गुणों को वहन करता है।

आदर्श गैस पदार्थ की वह अवस्था है जिसमें कणों की परस्पर क्रिया नगण्य होती है, अंतःक्रिया की स्थितिज ऊर्जा शून्य हो जाती है। केवल गति की ऊर्जा, जो कणों की गति पर निर्भर करती है, को ही महत्वपूर्ण माना जा सकता है।

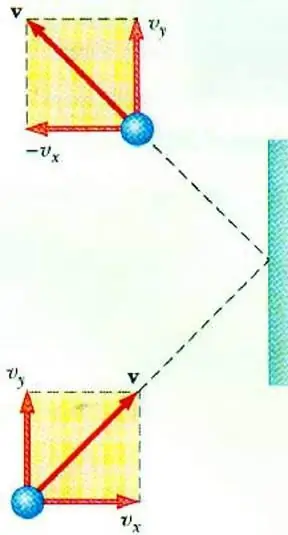
आदर्श गैस का दबाव

गैस के दबाव और उसके कणों की गति के बीच संबंध को प्रकट करने के लिए एक आदर्श गैस के एमकेटी के मूल समीकरण की अनुमति देता है। एक बर्तन में गतिमान एक कण, दीवार से टकराने पर, एक आवेग को स्थानांतरित करता है, जिसका मूल्य दूसरे नियम के आधार पर निर्धारित किया जा सकता हैन्यूटन:

फट=2मी₀वी_x

लोचदार प्रभाव के दौरान किसी कण के संवेग में परिवर्तन उसके वेग के क्षैतिज घटक में परिवर्तन से जुड़ा होता है। F दीवार पर कण की ओर से थोड़े समय के लिए कार्य करने वाला बल t है; एम₀ - कण द्रव्यमान।

सभी गैस कण समय ∆t के दौरान क्षेत्र S की सतह से टकराते हैं, सतह की दिशा में v_x गति से चलते हैं और मात्रा Sυ के सिलेंडर में स्थित होते हैं x Δt. कण सांद्रता n पर, ठीक आधे अणु दीवार की ओर बढ़ते हैं, अन्य आधे विपरीत दिशा में चलते हैं।

सभी कणों की टक्कर पर विचार करने के बाद, हम क्षेत्र पर कार्य करने वाले बल के लिए न्यूटन का नियम लिख सकते हैं:

F∆t=nm₀v_x²S∆t

चूंकि गैस के दबाव को सतह के लंबवत कार्य करने वाले बल के अनुपात के रूप में परिभाषित किया जाता है, इसलिए हम लिख सकते हैं:

पी=एफ: एस=एनएम₀वी_x²

एमकेटी के मूल समीकरण के रूप में परिणामी संबंध पूरे सिस्टम का वर्णन नहीं कर सकता, क्योंकि गति की केवल एक दिशा पर विचार किया जाता है।

मैक्सवेल वितरण

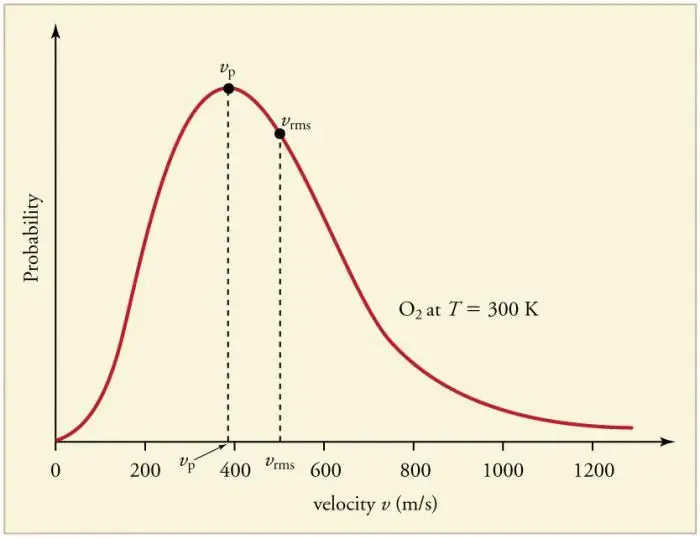
दीवारों और एक दूसरे के साथ गैस के कणों के लगातार लगातार टकराव से वेगों (ऊर्जा) के संदर्भ में कणों के एक निश्चित सांख्यिकीय वितरण की स्थापना होती है। सभी वेग सदिशों की दिशाएँ समान रूप से संभावित होती हैं। इस वितरण को मैक्सवेल वितरण कहा जाता है। 1860 में यह पैटर्न थाएमकेटी के आधार पर जे मैक्सवेल द्वारा व्युत्पन्न। वितरण कानून के मुख्य मापदंडों को वेग कहा जाता है: संभावित, वक्र के अधिकतम मूल्य के अनुरूप, और मूल-माध्य-वर्ग v_kv=√‹v² › - कण वेग का माध्य वर्ग।

गैस के तापमान में वृद्धि वेग में वृद्धि के अनुरूप है।

इस तथ्य के आधार पर कि सभी गति समान हैं, और उनके मॉड्यूल का मान समान है, हम यह मान सकते हैं:

‹v²›=‹v_x²› + ‹v y2^{› + v}z2^{›, से: वी}x2^›=v2^{›: 3}

गैस के दबाव के औसत मूल्य को ध्यान में रखते हुए एमकेटी का मूल समीकरण है:

p=एनएम₀‹v²›: 3.

यह संबंध इस मायने में अद्वितीय है कि यह सूक्ष्म मापदंडों के बीच संबंध को निर्धारित करता है: गति, कण द्रव्यमान, कण एकाग्रता और सामान्य रूप से गैस का दबाव।

कणों की गतिज ऊर्जा की अवधारणा का उपयोग करते हुए, एमकेटी के मूल समीकरण को अलग तरीके से फिर से लिखा जा सकता है:

p=2nm₀‹v²›: 6=2n‹E_k›: 3

किसी गैस का दाब उसके कणों की गतिज ऊर्जा के औसत मान के समानुपाती होता है।

तापमान

दिलचस्प बात यह है कि एक बंद बर्तन में गैस की निरंतर मात्रा के लिए, कोई गैस के दबाव और कण गति ऊर्जा के औसत मूल्य को जोड़ सकता है। इस मामले में, ऊर्जा को मापकर दबाव को मापा जा सकता हैकण।

क्या करें? गतिज ऊर्जा के साथ किस मूल्य की तुलना की जा सकती है? तापमान एक ऐसा मूल्य निकला।

तापमान पदार्थों की तापीय अवस्था का माप है। इसे मापने के लिए, एक थर्मामीटर का उपयोग किया जाता है, जिसका आधार गर्म होने पर काम कर रहे तरल पदार्थ (शराब, पारा) का थर्मल विस्तार होता है। थर्मामीटर स्केल प्रयोगात्मक रूप से बनाया गया है। आमतौर पर, एक स्थिर तापीय अवस्था (उबलते पानी, पिघलती बर्फ) पर होने वाली किसी भौतिक प्रक्रिया के दौरान काम कर रहे तरल पदार्थ की स्थिति के अनुरूप इस पर निशान लगाए जाते हैं। अलग-अलग थर्मामीटर के अलग-अलग पैमाने होते हैं। उदाहरण के लिए, सेल्सियस, फारेनहाइट।

सार्वभौम तापमान पैमाना

काम कर रहे तरल पदार्थ के गुणों से स्वतंत्रता के संदर्भ में गैस थर्मामीटर को अधिक दिलचस्प माना जा सकता है। उनका पैमाना इस्तेमाल की जाने वाली गैस के प्रकार पर निर्भर नहीं करता है। इस तरह के एक उपकरण में, कोई भी उस तापमान का अनुमान लगा सकता है जिस पर गैस का दबाव शून्य हो जाता है। गणना से पता चलता है कि यह मान -273.15 ^oC से मेल खाता है। तापमान पैमाना (पूर्ण तापमान पैमाना या केल्विन पैमाना) 1848 में पेश किया गया था। इस पैमाने के मुख्य बिंदु के रूप में शून्य गैस दबाव के संभावित तापमान को लिया गया था। पैमाने का एक इकाई खंड सेल्सियस पैमाने के एक इकाई मूल्य के बराबर होता है। गैस प्रक्रियाओं का अध्ययन करते समय तापमान का उपयोग करते हुए बुनियादी एमकेटी समीकरण को लिखना अधिक सुविधाजनक लगता है।

दबाव और तापमान के बीच संबंध

आनुभविक रूप से, आप इसे सत्यापित कर सकते हैंइसके तापमान के लिए गैस के दबाव की आनुपातिकता। उसी समय, यह पाया गया कि दबाव सीधे कणों की एकाग्रता के समानुपाती होता है:

पी=एनकेटी,

जहाँ T परम तापमान है, k एक स्थिरांक है 1.38•10^-23J/K.

मूल मान, जिसका सभी गैसों के लिए एक स्थिर मान होता है, बोल्ट्ज़मान स्थिरांक कहलाता है।

तापमान पर दबाव की निर्भरता और एमकेटी गैसों के मूल समीकरण की तुलना करते हुए, हम लिख सकते हैं:

‹E_k›=3kT: 2

गैस के अणुओं की गति की गतिज ऊर्जा का औसत मान उसके तापमान के समानुपाती होता है। अर्थात्, तापमान कण गति की गतिज ऊर्जा के माप के रूप में कार्य कर सकता है।