एक रैखिक फलन एक सतह के साथ खींची गई एक सीधी रेखा है। इसे विभिन्न प्रकारों और मॉडलों में विभाजित किया जा सकता है। नीचे हम इसे प्राप्त करने के सूत्रों पर विचार करेंगे, साथ ही विमान में इसकी पूर्णता को प्राप्त करेंगे। ड्रॉइंग में, आप इसे पूरी तरह से सत्यापित कर सकते हैं और समझ सकते हैं कि यह कैसा दिखना चाहिए।
रैखिक फलन y=kx + b
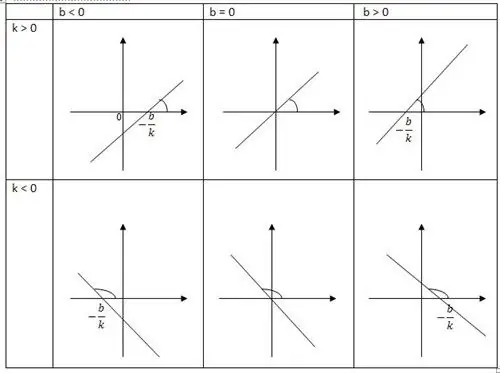
यह मान एक दृश्य में एक चर का सटीक माप है। वृद्धि एक रैखिक कार्य की मूल संपत्ति को संदर्भित करती है, यह वृद्धिशील तर्क के समानुपाती हो जाती है। दूसरे शब्दों में, फ़ंक्शन प्रत्यक्ष आनुपातिकता के सामान्यीकरण का प्रतिनिधित्व करता है। एक सीधी रेखा एक रैखिक कार्य का एक ग्राफ है। यहीं से इसका नाम आता है। एक वास्तविक चर दूसरे वास्तविक कार्य को स्पर्श करता है।
गुण
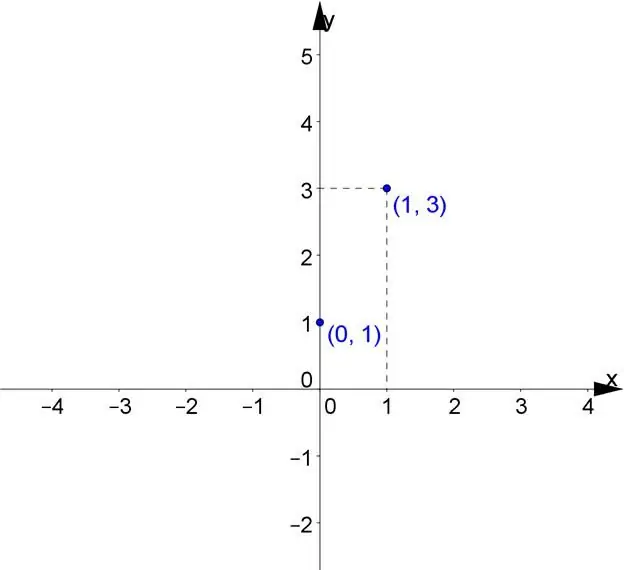
रैखिक फलन एक सीधी रेखा का जनक है, जिसमें x-अक्ष की धनात्मक दिशा होती है। इसके परिभाषित ढलान कारकों में से एक के है, यह कोण के स्पर्शरेखा को निर्धारित करता है। x-अक्ष की धनात्मक दिशा में बनी सीधी रेखा k है। अन्य निर्देशांक b इंगित करता हैबिंदु निर्देशांक, साथ ही अक्ष के साथ रेखा का प्रतिच्छेदन।
गैर-रैखिक कार्य क्या हैं?
ऐसे कार्य जो रैखिक नहीं होते, अरैखिक कहलाते हैं। यह चरों के बीच एक गणितीय संबंध है। नॉनलाइनियर को y=ax + b के रूप में व्यक्त नहीं किया जा सकता है। इस शब्द का प्रयोग उन क्षणों में किया जाता है जब सामान्य मामले का अध्ययन करना आवश्यक होता है। यह प्रक्रिया निचली डिग्री से शुरू होती है। इस मामले में, द्विघात सुधार पर विचार किया जाता है। ऐसे फलन में निरंतर वक्रता होती है।
माना गया गैर-रेखीय समीकरण मनमाना है। गैर-रैखिक फ़ंक्शन का एक उदाहरण y=x2 है। शब्द "रैखिक फ़ंक्शन" का उपयोग अक्सर शोधन और "सजातीय" के अतिरिक्त के साथ किया जाता है। इसे एक्स के सटीक रैखिक मानचित्रण पर लागू किया जा सकता है, जो एक वेक्टर स्पेस है। एक रेखीय फलन उसके समान संपूर्ण तंत्र है।






