गणित में, योग (बड़े ग्रीक सिग्मा प्रतीक द्वारा निरूपित) संख्याओं के योग का एक समूह है। राशि क्या है? यह इस तरह की कार्रवाई का परिणाम है। यदि संख्याओं को एक के बाद एक बाएँ से दाएँ जोड़ा जाता है, तो मध्यवर्ती परिणाम आंशिक योग होता है।
राशि क्या है?
योग की जाने वाली संख्याएँ पूर्णांक, परिमेय, वास्तविक या सम्मिश्र हो सकती हैं। उनके अलावा, अन्य प्रकार के मूल्यों को जोड़ा जा सकता है: वैक्टर, मैट्रिसेस, बहुपद, और किसी भी योजक समूह (या यहां तक कि एक मोनोइड) के सामान्य तत्वों में।
यदि पदों के तत्वों की संख्या सीमित है, तो योग हमेशा एक अच्छी तरह से परिभाषित मान देता है। मूल्यों के अनंत अनुक्रम के योग को एक श्रृंखला कहा जाता है। इसका मान अक्सर एक सीमा का उपयोग करके निर्धारित किया जा सकता है (हालाँकि कभी-कभी मान अनंत हो सकता है)।
अनुक्रम
संख्याओं के योग [3, 7, 2, 1] को एक व्यंजक द्वारा परिभाषित किया जा सकता है जिसका मान इसमें शामिल अंकों का योग है, उदाहरण के लिए 3 + 7 + 2 + 1=13. चूंकि योगसाहचर्य रूप से, योग इस बात पर निर्भर नहीं करता है कि शब्दों को कैसे समूहीकृत किया जाता है, उदाहरण के लिए, (3 + 7) + (2 + 1) और 3 + ((7 + 2) + 1) दोनों बराबर नौ हैं, इसलिए आमतौर पर कोष्ठकों को हटा दिया जाता है. जोड़ भी क्रमविनिमेय है, इसलिए शब्दों को पुनर्व्यवस्थित करने से योग का मूल्य नहीं बदलता है। ध्यान दें कि यह गुण अनंत योग के लिए काम नहीं कर सकता है।

इस तरह के दृश्यों के योग के लिए कोई विशेष अंकन नहीं है। दो तत्वों से कम होने पर केवल थोड़ी सी बारीकियां होती हैं। एक सदस्य के अनुक्रम के योग में एक प्लस चिह्न नहीं होता है (यह संख्या के रूप से अप्रभेद्य है), और यदि कोई तत्व नहीं हैं, तो इसे लिखा भी नहीं जा सकता है (बल्कि इसके बजाय इसे निरूपित किया जा सकता है इसका मान "0")। यदि, हालांकि, अनुक्रम की शर्तों को एक विशिष्ट पैटर्न द्वारा निर्दिष्ट किया जाता है, जैसे कि एक फ़ंक्शन, तो समन ऑपरेटर उपयोगी या आवश्यक भी हो सकता है।
रिकॉर्ड
यह समझने के लिए कि योग क्या है, इसके स्वरूप का विश्लेषण करना भी आवश्यक है।
1 से 100 तक के पूर्णांकों के अनुक्रम का योग करने के लिए, अक्सर एक व्यंजक का उपयोग किया जाता है जिसमें लापता सदस्यों को इंगित करने के लिए एक दीर्घवृत्त शामिल होता है: 1 + 2 + 3 + 4 + … + 99 + 100। पैटर्न है इस उदाहरण में देखने में काफी आसान है। हालांकि, अधिक जटिल विकल्पों के लिए, तत्वों के मूल्य को खोजने के लिए उपयोग किए जाने वाले नियम को निर्दिष्ट करना आवश्यक है, जिसे "Σ" सारांश ऑपरेटर का उपयोग करके प्राप्त किया जा सकता है। इस प्रतीक (सिग्मा) का उपयोग करके, आप निम्नलिखित संकेतन लागू कर सकते हैं:
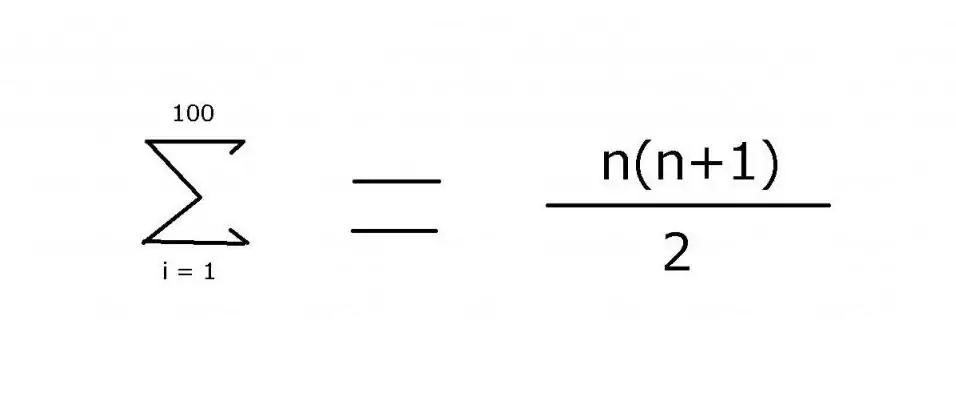
इस व्यंजक का मान 5050 है। इसे गणितीय प्रेरण का उपयोग करके पाया जा सकता है, जो कि सूत्र का दूसरा भाग है।
विभिन्न अनुक्रमों के लिए, सूत्र बदल जाएगा। रिकॉर्डिंग प्रक्रिया को कुछ अनंत अनुक्रम की पूर्व-छवि की खोज करने और फिर इसे एक सूत्र के साथ वर्णन करने के लिए कम कर दिया गया है। ऐसा करने के बाद, यह समझना मुश्किल नहीं है कि किसी विशेष मामले में राशि क्या है।
जब यह स्पष्ट करना आवश्यक हो कि संख्याओं को उनके चिह्नों (प्लस या माइनस) के साथ जोड़ा जाता है, तो बीजीय योग शब्द का प्रयोग किया जाता है। उदाहरण के लिए, इलेक्ट्रिकल सर्किट सिद्धांत में, किरचॉफ के सर्किट कानून एक बिंदु पर मिलने वाले कंडक्टरों के नेटवर्क में धाराओं के बीजगणितीय योग पर विचार करते हैं, जो एक नोड में और बाहर बहने वाली धाराओं के विपरीत संकेत देते हैं।






