भौतिकी में परिभाषाओं का ज्ञान विभिन्न शारीरिक समस्याओं को सफलतापूर्वक हल करने के लिए एक महत्वपूर्ण कारक है। लेख में, हम विचार करेंगे कि एक आदर्श गैस प्रणाली के लिए समदाब रेखीय, समस्थानिक, समतापीय और रुद्धोष्म प्रक्रियाओं का क्या अर्थ है।
आदर्श गैस और उसका समीकरण
आइसोबैरिक, आइसोकोरिक और इज़ोटेर्मल प्रक्रियाओं के विवरण पर आगे बढ़ने से पहले, आइए विचार करें कि एक आदर्श गैस क्या है। भौतिकी में इस परिभाषा के तहत वे एक ऐसी प्रणाली पर विचार करते हैं जिसमें बड़ी संख्या में आयामहीन और गैर-अंतःक्रियात्मक कण होते हैं जो सभी दिशाओं में उच्च गति से चलते हैं। दरअसल, हम बात कर रहे हैं पदार्थ की एक गैसीय समुच्चय अवस्था के बारे में, जिसमें परमाणुओं और अणुओं के बीच की दूरी उनके आकार से कहीं अधिक हो जाती है और जिसमें गतिज ऊर्जा की तुलना में कणों के परस्पर क्रिया की स्थितिज ऊर्जा की उनके लघुता के कारण उपेक्षा की जाती है।
एक आदर्श गैस की अवस्था उसके थर्मोडायनामिक मापदंडों की समग्रता होती है। मुख्य हैं तापमान, आयतन और दबाव। आइए उन्हें क्रमशः टी, वी और पी अक्षरों से निरूपित करें। XIX सदी के 30 के दशक मेंक्लैपेरॉन (एक फ्रांसीसी वैज्ञानिक) ने सबसे पहले एक समीकरण लिखा था जो संकेतित थर्मोडायनामिक मापदंडों को एक समानता के भीतर जोड़ता है। ऐसा लगता है:
पीवी=एनआरटी,
जहाँ n और R क्रमशः पदार्थों की मात्रा और गैस स्थिरांक हैं।
गैसों में आइसोप्रोसेस क्या हैं?
जैसा कि कई लोगों ने देखा है, आइसोबैरिक, आइसोकोरिक और इज़ोटेर्मल प्रक्रियाएं अपने नामों में एक ही "आइसो" उपसर्ग का उपयोग करती हैं। इसका मतलब पूरी प्रक्रिया के पारित होने के दौरान एक थर्मोडायनामिक पैरामीटर की समानता है, जबकि शेष पैरामीटर बदलते हैं। उदाहरण के लिए, एक इज़ोटेर्मल प्रक्रिया इंगित करती है कि, परिणामस्वरूप, सिस्टम का निरपेक्ष तापमान स्थिर बना रहता है, जबकि एक आइसोकोरिक प्रक्रिया एक स्थिर आयतन को इंगित करती है।
इसोप्रोसेस का अध्ययन करना सुविधाजनक है, क्योंकि थर्मोडायनामिक मापदंडों में से एक को ठीक करने से गैस अवस्था के सामान्य समीकरण का सरलीकरण होता है। यह ध्यान रखना महत्वपूर्ण है कि इन सभी आइसोप्रोसेस के लिए गैस कानूनों को प्रयोगात्मक रूप से खोजा गया था। उनके विश्लेषण ने क्लैपेरॉन को कम सार्वत्रिक समीकरण प्राप्त करने की अनुमति दी।
आइसोबैरिक, आइसोकोरिक और इज़ोटेर्मल प्रक्रियाएं
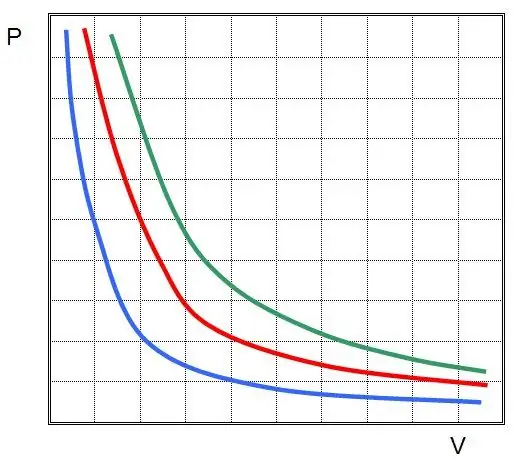
एक आदर्श गैस में समतापी प्रक्रम के लिए प्रथम नियम की खोज की गई। अब इसे बॉयल-मैरियट नियम कहते हैं। चूंकि T नहीं बदलता है, इसलिए राज्य का समीकरण समानता का तात्पर्य है:
पीवी=कास्ट.
दूसरे शब्दों में, यदि गैस का तापमान स्थिर रखा जाता है, तो सिस्टम में दबाव में कोई भी परिवर्तन इसके आयतन में व्युत्क्रमानुपाती परिवर्तन की ओर ले जाता है। फलन P(V) का आलेख हैअतिशयोक्ति।
समद्विबाहु प्रक्रम - यह तंत्र की स्थिति में परिवर्तन है, जिसमें दाब स्थिर रहता है। Clapeyron समीकरण में P का मान निश्चित करने के बाद, हम निम्नलिखित कानून प्राप्त करते हैं:
वी/टी=कास्ट.
यह समानता फ्रांसीसी भौतिक विज्ञानी जैक्स चार्ल्स के नाम पर है, जिन्होंने इसे 18वीं शताब्दी के अंत में प्राप्त किया था। आइसोबार (वी (टी) फ़ंक्शन का ग्राफिक प्रतिनिधित्व) एक सीधी रेखा की तरह दिखता है। सिस्टम में जितना अधिक दबाव होता है, यह रेखा उतनी ही तेजी से ऊपर उठती है।
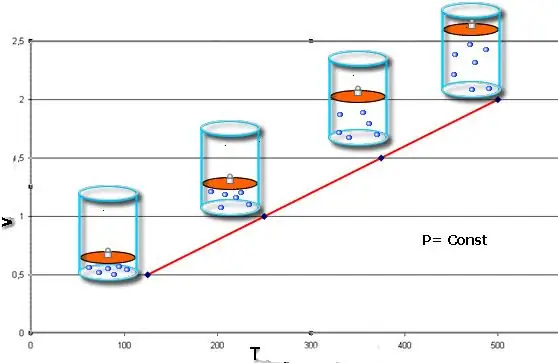
अगर पिस्टन के नीचे गैस को गर्म किया जाता है तो आइसोबैरिक प्रक्रिया को लागू करना आसान होता है। उत्तरार्द्ध के अणु अपनी गति (गतिज ऊर्जा) बढ़ाते हैं, पिस्टन पर एक उच्च दबाव बनाते हैं, जिससे गैस का विस्तार होता है और पी का निरंतर मूल्य बना रहता है।
आखिरकार, तीसरा आइसोप्रोसेस आइसोकोरिक है। यह निरंतर मात्रा के साथ चलता है। राज्य के समीकरण से हम संबंधित समानता प्राप्त करते हैं:
पी/टी=कास्ट.
इसे भौतिकविदों के बीच गे-लुसाक के नियम के रूप में जाना जाता है। दबाव और निरपेक्ष तापमान के बीच प्रत्यक्ष आनुपातिकता इंगित करती है कि समद्विबाहु प्रक्रिया का ग्राफ, समदाब रेखीय के ग्राफ की तरह, एक सकारात्मक ढलान के साथ एक सीधी रेखा है।
यह समझना महत्वपूर्ण है कि सभी आइसोप्रोसेस बंद सिस्टम में होते हैं, अर्थात n का मान उनके पाठ्यक्रम के दौरान संरक्षित रहता है।
रुद्धोष्म प्रक्रिया
यह प्रक्रिया "आइसो" श्रेणी से संबंधित नहीं है, क्योंकि इसके पारित होने के दौरान सभी तीन थर्मोडायनामिक पैरामीटर बदल जाते हैं। स्थिरोष्मप्रणाली के दो राज्यों के बीच संक्रमण कहा जाता है, जिसमें यह पर्यावरण के साथ गर्मी का आदान-प्रदान नहीं करता है। इस प्रकार, सिस्टम का विस्तार इसके आंतरिक ऊर्जा भंडार के कारण होता है, जिससे इसमें दबाव और पूर्ण तापमान में उल्लेखनीय गिरावट आती है।
एक आदर्श गैस के लिए रुद्धोष्म प्रक्रम का वर्णन पॉइसन समीकरण द्वारा किया जाता है। उनमें से एक नीचे दिखाया गया है:
पीवीγ=कास्ट,
जहां γ स्थिर दबाव और स्थिर आयतन पर ताप क्षमता का अनुपात है।
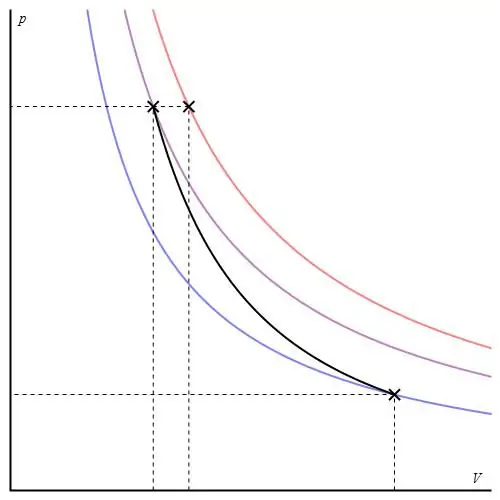
एडियाबेटिक ग्राफ आइसोकोरिक प्रक्रिया ग्राफ और आइसोबैरिक ग्राफ से अलग है, लेकिन यह हाइपरबोला (आइसोथर्म) के समान है। पी-वी अक्षों में रूद्धोष्म समतापी की तुलना में अधिक तीक्ष्ण व्यवहार करता है।






