ऊष्मागतिकी के दृष्टिकोण से गैसों का वर्णन मैक्रोस्कोपिक विशेषताओं के एक समूह द्वारा किया जाता है, जिनमें से मुख्य तापमान, दबाव और आयतन हैं। इन मापदंडों में से एक की स्थिरता और अन्य दो में परिवर्तन इंगित करता है कि गैस में एक या दूसरा आइसोप्रोसेस होता है। हम इस लेख को प्रश्नों के विस्तृत उत्तर के लिए समर्पित करेंगे कि यह एक आइसोकोरिक प्रक्रिया है, यह गैस प्रणाली के राज्यों में इज़ोटेर्मल और आइसोबैरिक परिवर्तनों से कैसे भिन्न है।
भौतिकी में आदर्श गैस

इस प्रश्न का उत्तर देने से पहले कि यह एक समद्विबाहु प्रक्रिया है, आपको एक आदर्श गैस की अवधारणा को बेहतर तरीके से जानना चाहिए। भौतिकी में, इसे किसी भी गैस के रूप में समझा जाता है जिसमें इसके घटक कणों की औसत गतिज ऊर्जा उनकी बातचीत की संभावित ऊर्जा से कहीं अधिक होती है, और इन कणों के बीच की दूरी उनके रैखिक आयामों से बड़े परिमाण के कई क्रम हैं। विख्यात शर्तों के तहत, यह संभव है, जब बाहर ले जाया जाता हैगणना कणों के बीच परस्पर क्रिया ऊर्जा को ध्यान में नहीं रखती है (यह शून्य के बराबर है), और यह भी माना जा सकता है कि कण एक निश्चित द्रव्यमान m वाले भौतिक बिंदु हैं।
एक आदर्श गैस में होने वाली एकमात्र प्रक्रिया पदार्थ वाले बर्तन की दीवारों के साथ कणों की टक्कर है। ये टकराव व्यवहार में खुद को गैस पी में एक निश्चित दबाव के अस्तित्व के रूप में प्रकट करते हैं।
एक नियम के रूप में, कोई भी गैसीय पदार्थ जिसमें अपेक्षाकृत रासायनिक रूप से निष्क्रिय अणु होते हैं और जिसमें कम दबाव और उच्च तापमान होता है, व्यावहारिक गणना के लिए पर्याप्त सटीकता के साथ एक आदर्श गैस माना जा सकता है।
एक आदर्श गैस का वर्णन करने वाला समीकरण
बेशक, हम बात कर रहे हैं क्लैपेरॉन-मेंडेलीव के सार्वभौमिक नियम के बारे में, जिसे समझने के लिए इसे अच्छी तरह से समझना चाहिए कि यह एक समद्विबाहु प्रक्रिया है। तो, राज्य के सार्वभौम समीकरण के निम्नलिखित रूप हैं:
पीवी=एनआरटी.
अर्थात, दबाव P का गुणनफल और गैस का आयतन V, परम तापमान T के गुणनफल और मोल n में पदार्थ की मात्रा के बराबर है, जहाँ R आनुपातिकता कारक है। समीकरण को पहली बार 1834 में एमिल क्लैपेरॉन द्वारा लिखा गया था, और 19 वीं शताब्दी के 70 के दशक में, डी। मेंडेलीव ने इसे एक एकल सार्वभौमिक गैस स्थिरांक R (8.314 J/(molK) के निरंतर मूल्यों के एक सेट में बदल दिया।)).
क्लैपेरॉन-मेंडेलीव समीकरण के अनुसार, एक बंद प्रणाली में गैस कणों की संख्या स्थिर रहती है, इसलिए केवल तीन मैक्रोस्कोपिक पैरामीटर बदल सकते हैं (टी, पी)और वी)। बाद वाला तथ्य विभिन्न आइसोप्रोसेसेस की समझ को रेखांकित करता है जिसकी चर्चा नीचे की जाएगी।
आइसोकोरिक प्रक्रिया क्या है?
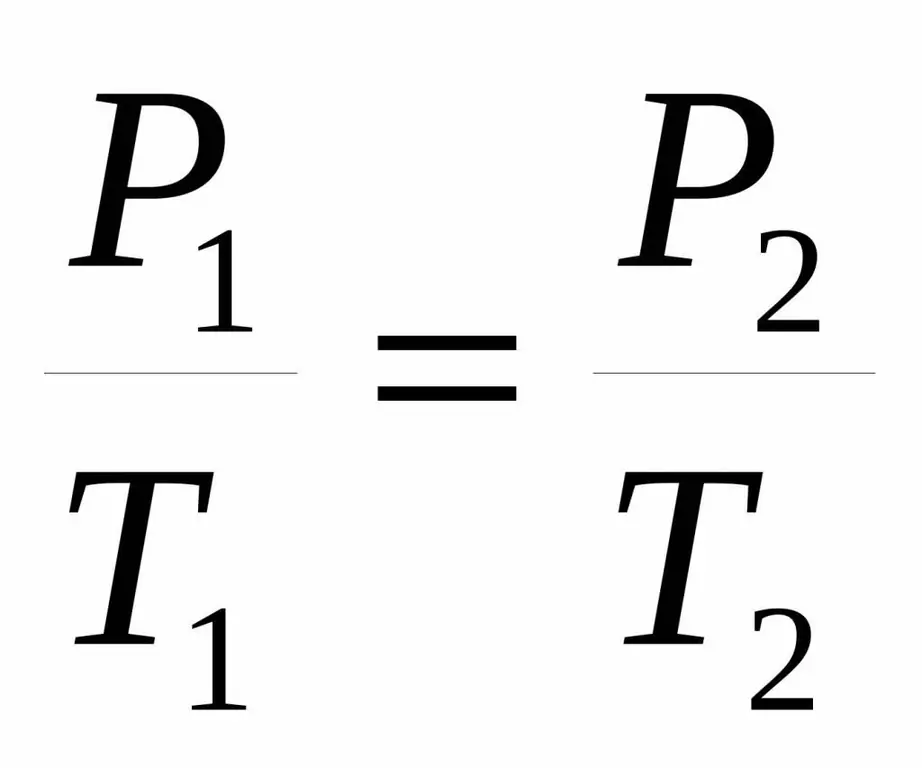
इस प्रक्रिया को सिस्टम की स्थिति में होने वाले किसी भी परिवर्तन के रूप में समझा जाता है, जिसमें इसकी मात्रा संरक्षित होती है।
यदि हम राज्य के सार्वभौम समीकरण की ओर मुड़ें, तो हम कह सकते हैं कि एक समद्विबाहु प्रक्रिया में गैस में केवल दबाव और पूर्ण तापमान में परिवर्तन होता है। यह समझने के लिए कि थर्मोडायनामिक पैरामीटर कैसे बदलते हैं, हम संबंधित गणितीय अभिव्यक्ति लिखते हैं:
पी / टी=कास्ट।
कभी-कभी यह समानता थोड़े अलग रूप में दी जाती है:
पी1 / टी1=पी2 / टी 2.
दोनों समानताएं एक फ्रांसीसी वैज्ञानिक के नाम पर चार्ल्स का नियम कहलाती हैं, जिन्होंने 18वीं शताब्दी के अंत में प्रयोगात्मक रूप से विख्यात निर्भरता प्राप्त की थी।

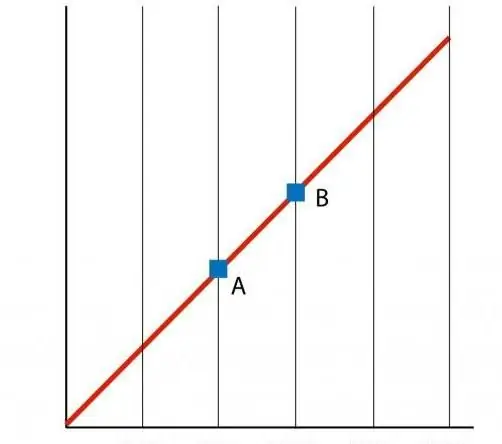
अगर हम फंक्शन P(T) का ग्राफ बनाते हैं, तो हमें एक सीधी रेखा पर निर्भरता मिलती है, जिसे आइसोकोर कहा जाता है। कोई भी समस्थानिक (n और V के सभी मानों के लिए) एक सीधी रेखा है।
प्रक्रिया का ऊर्जा विवरण
जैसा कि उल्लेख किया गया है, एक आइसोकोरिक प्रक्रिया एक प्रणाली की स्थिति में परिवर्तन है जो एक बंद लेकिन पृथक प्रणाली में नहीं होती है। हम गैस और पर्यावरण के बीच हीट एक्सचेंज की संभावना के बारे में बात कर रहे हैं। सामान्य तौर पर, सिस्टम को ऊष्मा Q की कोई भी आपूर्ति दो परिणामों की ओर ले जाती है:
- आंतरिक ऊर्जा U को बदलता है;
- गैसकाम करता है ए, विस्तार या अनुबंध।
अंतिम निष्कर्ष गणितीय रूप से इस प्रकार लिखा गया है:
क्यू=यू + ए.
एक आदर्श गैस की आइसोकोरिक प्रक्रिया, इसकी परिभाषा के अनुसार, गैस द्वारा किया गया कार्य नहीं है, क्योंकि इसका आयतन अपरिवर्तित रहता है। इसका मतलब है कि सिस्टम को आपूर्ति की जाने वाली सारी गर्मी इसकी आंतरिक ऊर्जा को बढ़ाने के लिए जाती है:
क्यू=यू.
यदि हम इस अभिव्यक्ति में आंतरिक ऊर्जा के लिए स्पष्ट सूत्र को प्रतिस्थापित करते हैं, तो आइसोकोरिक प्रक्रिया की गर्मी को इस प्रकार दर्शाया जा सकता है:
क्यू=जेड/2एनआरटी.
यहाँ z स्वतंत्रता की डिग्री की संख्या है, जो गैस बनाने वाले अणुओं की बहुपरमाणुक प्रकृति से निर्धारित होती है। एक परमाणु गैस के लिए, z=3, एक द्विपरमाणुक गैस के लिए - 5, और एक त्रिपरमाणुक और अधिक के लिए - 6. यहाँ, स्वतंत्रता की डिग्री के तहत, हमारा मतलब अनुवाद और घूर्णी डिग्री है।
यदि हम समद्विबाहु और समदाबीय प्रक्रियाओं में गैस प्रणाली को गर्म करने की दक्षता की तुलना करते हैं, तो पहले मामले में हमें अधिकतम दक्षता प्राप्त होगी, क्योंकि प्रणाली की स्थिति में समदाब रेखीय परिवर्तन के दौरान, गैस फैलती है, और गर्मी इनपुट का एक हिस्सा काम करने में खर्च होता है।
आइसोबैरिक प्रक्रिया
ऊपर हमने विस्तार से वर्णन किया है कि यह एक समद्विबाहु प्रक्रिया है। अब आइए अन्य आइसोप्रोसेसेस के बारे में कुछ शब्द कहें। आइए आइसोबैरिक से शुरू करते हैं। नाम के आधार पर इसे निरंतर दबाव में राज्यों के बीच प्रणाली के संक्रमण के रूप में समझा जाता है। इस प्रक्रिया को गे-लुसाक कानून द्वारा इस प्रकार वर्णित किया गया है:
वी / टी=कास्ट।
आइसोकोर की तरह, V(T) समद्विबाहु भी ग्राफ पर एक सीधी रेखा का प्रतिनिधित्व करता है।
के लिएकिसी भी समदाब रेखीय प्रक्रिया में, गैस द्वारा किए गए कार्य की गणना करना सुविधाजनक होता है, क्योंकि यह स्थिर दबाव और आयतन में परिवर्तन के गुणनफल के बराबर होता है।
समतापी प्रक्रिया
यह एक ऐसी प्रक्रिया है जिसमें सिस्टम का तापमान स्थिर रहता है। यह बॉयल-मैरियोट कानून द्वारा एक आदर्श गैस के लिए वर्णित है। यह ध्यान देने योग्य है कि यह पहला प्रयोगात्मक रूप से खोजा गया गैस कानून है (17 वीं शताब्दी का दूसरा भाग)। इसका गणितीय अंकन इस तरह दिखता है:
पीवी=कास्ट.
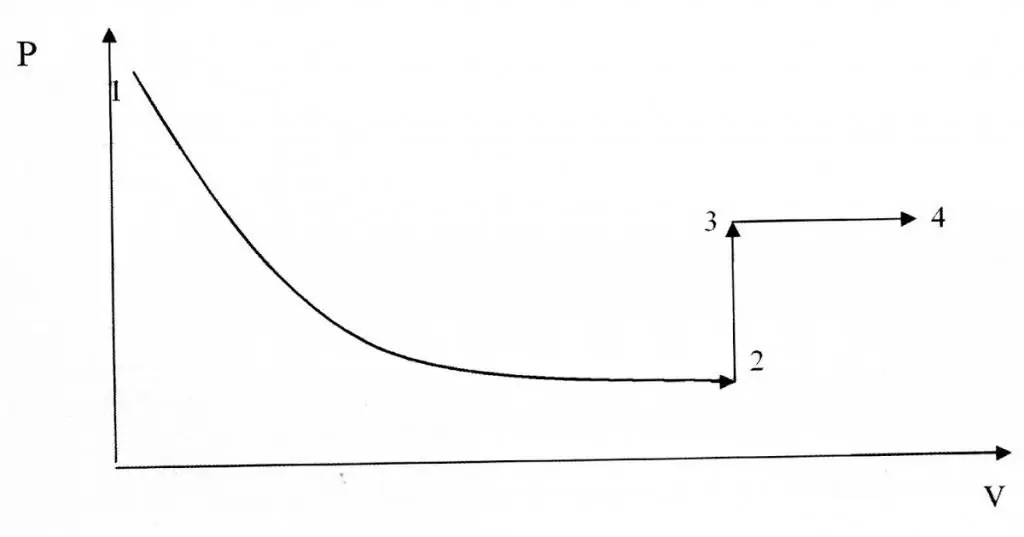
आइसोकोरिक और इज़ोटेर्मल प्रक्रियाएं उनके चित्रमय प्रतिनिधित्व के संदर्भ में भिन्न होती हैं, क्योंकि फ़ंक्शन P(V) एक अतिपरवलयिक है, रैखिक संबंध नहीं।
समस्या समाधान का उदाहरण
आइए एक व्यावहारिक समस्या को हल करने के लिए उनके आवेदन द्वारा लेख में प्रदान की गई सैद्धांतिक जानकारी को समेकित करें। यह ज्ञात है कि शुद्ध गैसीय नाइट्रोजन एक सिलेंडर में 1 वायुमंडल के दबाव और 25 डिग्री सेल्सियस के तापमान पर था। गैस सिलेंडर को गर्म करने और उसमें दबाव मापने के बाद, यह 1.5 वायुमंडल निकला। सिलेंडर को गर्म करने के बाद गैस का तापमान कितना होता है? यदि गुब्बारे में 4 मोल नाइट्रोजन हो तो गैस की आंतरिक ऊर्जा कितनी मात्रा में बदल जाती है।
पहले प्रश्न का उत्तर देने के लिए, हम निम्नलिखित अभिव्यक्ति का उपयोग करते हैं:
पी1 / टी1=पी2 / टी 2.
जहां से हमें मिलता है:
टी2=पी2 / पी1 टी 1.
इस अभिव्यक्ति में, दबाव को मनमानी इकाइयों में प्रतिस्थापित किया जा सकता हैमाप, क्योंकि वे सिकुड़ रहे हैं, और तापमान केवल केल्विन में है। इसके साथ ही, हमें मिलता है:
टी2=1.5 /1298.15=447.224 के.
डिग्री सेल्सियस में परिकलित तापमान 174 डिग्री सेल्सियस है।
चूंकि नाइट्रोजन अणु द्विपरमाणुक है, गर्म करने के दौरान इसकी आंतरिक ऊर्जा में परिवर्तन निम्नानुसार निर्धारित किया जा सकता है:
ΔU=5/2nRT.
ज्ञात मानों को इस व्यंजक में प्रतिस्थापित करने पर हमें समस्या के दूसरे प्रश्न का उत्तर मिलेगा: U=+12.4 kJ.






