जब सहकर्मी समीक्षा, उदाहरण के लिए, उत्पादों की प्रतिस्पर्धात्मकता का आकलन करना, यह आवश्यक है, जैसा कि किसी भी वैज्ञानिक कार्य में, सांख्यिकीय डेटा प्रोसेसिंग को अंजाम देना है। उत्तरार्द्ध विशेषज्ञ राय की स्थिरता को निर्धारित करने के साथ शुरू होता है, जिसकी संख्यात्मक अभिव्यक्ति समवर्ती गुणांक है।
हमें एक विशेषज्ञ आम सहमति मूल्यांकन की आवश्यकता क्यों है?
यह आकलन सबसे पहले जरूरी है, क्योंकि अनुमानित मापदंडों पर विशेषज्ञों की राय काफी भिन्न हो सकती है। प्रारंभ में, संकेतकों की रैंकिंग करके और उन्हें महत्व (वजन) का एक निश्चित गुणांक निर्दिष्ट करके मूल्यांकन किया जाता है। इन गुणांकों में असंगत रैंकिंग परिणाम सांख्यिकीय रूप से अविश्वसनीय हैं। विशेषज्ञों की राय उनकी आवश्यक संख्या (7-10 से अधिक) के साथ सामान्य कानून के अनुसार वितरित की जानी चाहिए।
समन्वय के गुणांक की अवधारणा
तो। संगति समरूपता है। गुणांक एक आयामहीन मात्रा है जो सामान्य स्थिति में फैलाव के अधिकतम फैलाव के अनुपात को दर्शाता है। आइए इन अवधारणाओं का सामान्यीकरण करें।
समन्वय गुणांक 0 से 1 तक की संख्या है, जो विशेषज्ञ राय की निरंतरता को दर्शाता है जबकुछ संपत्तियों की रैंकिंग। यह मान 0 के जितना करीब होगा, संगति उतनी ही कम मानी जाएगी। यदि इस गुणांक का मान 0.3 से कम है, तो विशेषज्ञों की राय असंगत मानी जाती है। जब गुणांक का मान 0.3 से 0.7 की सीमा में होता है, तो संगति को औसत माना जाता है। 0.7 से अधिक के मान को उच्च स्थिरता माना जाता है।
मामलों का प्रयोग करें
सांख्यिकीय अनुसंधान करते समय, ऐसी स्थितियाँ उत्पन्न हो सकती हैं जिनमें किसी वस्तु को दो अनुक्रमों द्वारा नहीं दिखाया जा सकता है, जो कि समवर्ती गुणांक का उपयोग करके सांख्यिकीय रूप से संसाधित होते हैं, लेकिन कई अनुक्रमों द्वारा, जो तदनुसार समान स्तर के विशेषज्ञों द्वारा क्रमबद्ध होते हैं। एक निश्चित क्षेत्र में व्यावसायिकता।
विशेषज्ञों द्वारा की गई रैंकिंग की निरंतरता को इस परिकल्पना की शुद्धता की पुष्टि करने के लिए निर्धारित किया जाना चाहिए कि विशेषज्ञ अपेक्षाकृत सटीक माप करते हैं, जो विशेषज्ञ समूहों में विभिन्न समूहों के गठन की अनुमति देता है, जो बड़े पैमाने पर मानव कारकों द्वारा निर्धारित होते हैं, मुख्य रूप से जैसे विचारों, अवधारणाओं, विभिन्न वैज्ञानिक स्कूलों, पेशेवर गतिविधि की प्रकृति आदि में अंतर।
रैंक पद्धति का संक्षिप्त विवरण। इसके फायदे और नुकसान
रैंकिंग करते समय, रैंक पद्धति का उपयोग किया जाता है। इसका सार इस तथ्य में निहित है कि वस्तु की प्रत्येक संपत्ति को अपनी विशिष्ट रैंक सौंपी जाती है। इसके अलावा, विशेषज्ञ समूह में शामिल प्रत्येक विशेषज्ञ को यह रैंक सौंपी जाती हैस्वतंत्र रूप से, जिसके परिणामस्वरूप विशेषज्ञ राय की स्थिरता की पहचान करने के लिए इन डेटा को संसाधित करने की आवश्यकता होती है। यह प्रक्रिया समरूपता के गुणांक की गणना करके की जाती है।
रैंक पद्धति का मुख्य लाभ इसके कार्यान्वयन में आसानी है।
विधि के मुख्य नुकसान हैं:
- रैंकिंग ऑब्जेक्ट्स की एक छोटी संख्या, क्योंकि जब उनकी संख्या 15-20 से अधिक हो जाती है, तो ऑब्जेक्टिव रैंकिंग स्कोर निर्दिष्ट करना मुश्किल हो जाता है;
- इस पद्धति के प्रयोग के आधार पर यह प्रश्न खुला रहता है कि अध्ययन की गई वस्तुएँ एक दूसरे से कितनी दूर महत्व रखती हैं।
इस पद्धति का उपयोग करते समय, यह ध्यान में रखा जाना चाहिए कि रेटिंग किसी प्रकार के संभाव्य मॉडल पर आधारित हैं, इसलिए उन्हें गुंजाइश को देखते हुए सावधानी के साथ लागू किया जाना चाहिए।
केंडल का कॉनकॉर्डेंस रैंक गुणांक
सजातीय वस्तुओं की विशेषता वाली मात्रात्मक और गुणात्मक विशेषताओं के बीच संबंध को निर्धारित करने के लिए उपयोग किया जाता है और उसी सिद्धांत के अनुसार रैंक किया जाता है।
यह गुणांक सूत्र द्वारा निर्धारित किया जाता है:
t=2S/(n(n-1)), जहां
S - दूसरी विशेषता पर अनुक्रमों की संख्या और व्युत्क्रमों की संख्या के बीच अंतर का योग;
n - प्रेक्षणों की संख्या।

गणना एल्गोरिथ्म:
- x मानों को आरोही या अवरोही क्रम में स्थान दिया गया है।
- y-मानों को उस क्रम में व्यवस्थित किया जाता है जिसमें वे x-मानों के अनुरूप होते हैं.
- y के प्रत्येक क्रमिक रैंक के लिए, निर्धारित करें कि कितने उच्च रैंक मान इसका अनुसरण करते हैं। उन्हें जोड़ा जाता है और x और y में रैंकों के अनुक्रमों के पत्राचार की माप की गणना की जाती है।
- इसी प्रकार, निम्न मान वाले y के रैंकों की संख्या की गणना की जाती है, जो भी जोड़ते हैं।
- उच्च मूल्यों के साथ रैंकों की संख्या और कम मूल्यों के साथ रैंकों की संख्या जोड़ें, जिसके परिणामस्वरूप मूल्य एस होता है।
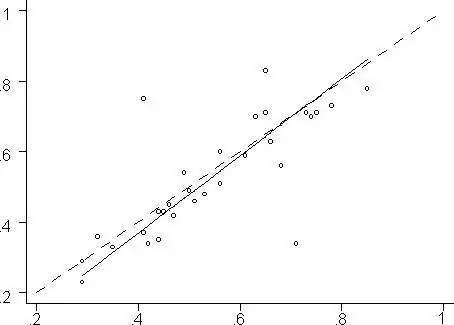
यह गुणांक दो चरों के बीच संबंध को दर्शाता है, और ज्यादातर मामलों में इसे केंडल रैंक सहसंबंध गुणांक कहा जाता है। इस तरह की निर्भरता को ग्राफिक रूप से दर्शाया जा सकता है।
गुणांक का निर्धारण
यह कैसे किया जाता है? यदि रैंक की गई विशेषताओं या कारकों की संख्या 2 से अधिक है, तो समवर्ती गुणांक का उपयोग किया जाता है, जो संक्षेप में, रैंक सहसंबंध का एक बहु प्रकार है।
सावधान रहें। समवर्ती गुणांक की गणना, रैंकों के वर्गों के योग के विचलन के अनुपात पर आधारित होती है, जो रैंकों के वर्गों के औसत योग से, 12 से गुणा करके, विशेषज्ञों के वर्ग में, संख्या के घन के बीच के अंतर से गुणा की जाती है। वस्तुओं की संख्या और वस्तुओं की संख्या।
गणना एल्गोरिथ्म
यह समझने के लिए कि गणना सूत्र के अंश में 12 नंबर कहाँ से आता है, आइए निर्धारण एल्गोरिथ्म को देखें।
एक निश्चित विशेषज्ञ के रैंक वाली प्रत्येक पंक्ति के लिए, रैंकों के योग की गणना की जाती है, जो एक यादृच्छिक मान है।
समन्वय गुणांक को आम तौर पर विचरण अनुमान (डी) के अनुपात के रूप में परिभाषित किया जाता है जो विचरण अनुमान के अधिकतम मूल्य के लिए होता है(डीअधिकतम)। आइए हम इन राशियों की परिभाषाएँ क्रमिक रूप से बनाएँ।
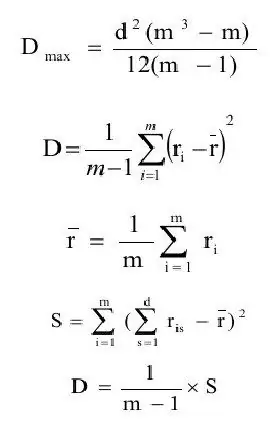
जहां आरऔसत - उम्मीद का अनुमान;
मी - वस्तुओं की संख्या।
डी से डी के संबंध में परिणामी फ़ार्मुलों को प्रतिस्थापित करनाअधिकतम हमें कॉनकॉर्डेंस गुणांक के लिए अंतिम सूत्र मिलता है:
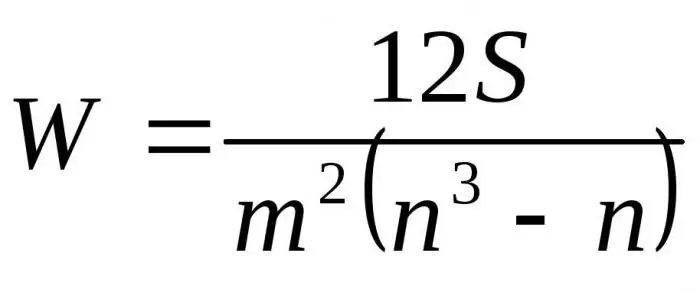
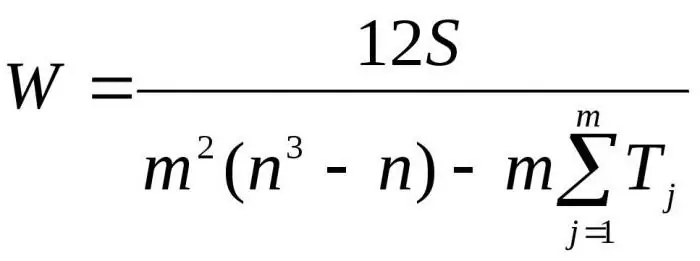
यहाँ m विशेषज्ञों की संख्या है, n वस्तुओं की संख्या है।
यदि संबंधित रैंक नहीं हैं तो पहले सूत्र का उपयोग समवर्ती कारक निर्धारित करने के लिए किया जाता है। यदि संबंधित रैंक हैं तो दूसरे सूत्र का उपयोग किया जाता है।
तो, समवर्ती गुणांक की गणना समाप्त हो गई है। आगे क्या होगा? इस गुणांक को विशेषज्ञों की संख्या और स्वतंत्रता की डिग्री (एम -1) से गुणा करके पियरसन गुणांक का उपयोग करके प्राप्त मूल्य का मूल्यांकन महत्व के लिए किया जाता है। परिणामी मानदंड की तुलना तालिका मान के साथ की जाती है, और यदि पहले का मान अंतिम से अधिक है, तो वे अध्ययन के तहत गुणांक के महत्व की बात करते हैं।
संबंधित रैंकों के मामले में, पियर्सन मानदंड की गणना कुछ अधिक जटिल हो जाती है और निम्नलिखित अनुपात द्वारा की जाती है: (12S)/(d(m2+) एम)-(1/(एम-1))x(टीs1 + टीs2 + टीsn)
उदाहरण
मान लें कि विशेषज्ञ विधि खुदरा नेटवर्क में बेचे जाने वाले मक्खन की प्रतिस्पर्धात्मकता का मूल्यांकन करती है। आइए हम समवर्ती गुणांक की गणना का एक उदाहरण दें। प्रतिस्पर्धात्मकता का आकलन करने से पहले, उपभोक्ता को रैंक करना आवश्यक हैइस उत्पाद के गुण जो मूल्यांकन में शामिल हैं। आइए मान लें कि ये गुण निम्नलिखित होंगे: स्वाद और गंध, स्थिरता और उपस्थिति, रंग, पैकेजिंग और लेबलिंग, वसा सामग्री, व्यापार नाम, निर्माता, मूल्य।
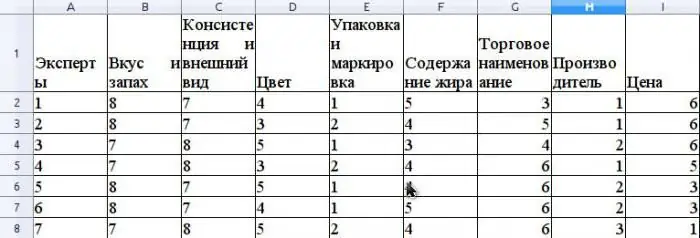
मान लें कि विशेषज्ञ समूह में 7 विशेषज्ञ हैं। यह आंकड़ा इन गुणों की रैंकिंग के परिणाम दिखाता है।
r का औसत मान अंकगणितीय औसत के रूप में परिकलित किया जाता है और यह 31.5 होगा। S को खोजने के लिए, ris और r औसत के बीच के वर्ग अंतर को सूत्र के अनुसार जोड़ दें ऊपर, और निर्धारित करें कि S का मान 1718 है।
संबंधित रैंकों का उपयोग किए बिना सूत्र का उपयोग करके समवर्ती गुणांक की गणना करें (रैंक संबंधित होंगे यदि एक ही विशेषज्ञ सलाहकार के पास विभिन्न गुणों के लिए समान रैंक हों)।
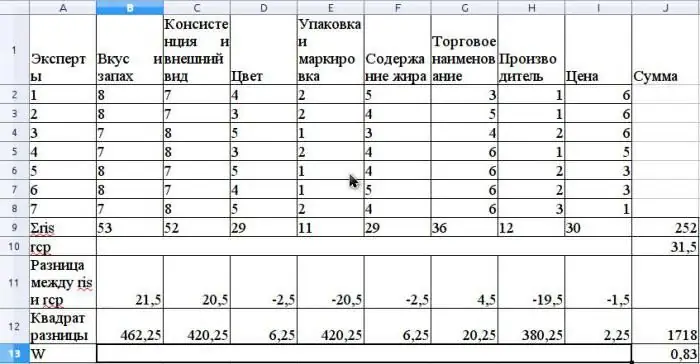
इस गुणांक का मान 0.83 होगा। यह विशेषज्ञों के बीच एक मजबूत सहमति को दर्शाता है।
पियर्सन परीक्षण का उपयोग करके इसके महत्व की जाँच करें:
7 x 0.83 x (8-1)=40.7.
पियर्सन का सारणी परीक्षण 1% महत्व स्तर पर 18.5 है, और 5% -14.1 पर है।.
उदाहरण गणितीय गणनाओं की मूल बातें जानने वाले किसी भी व्यक्ति के लिए गणना की सरलता और पहुंच को दर्शाता है। उन्हें कम करने के लिए,स्प्रेडशीट फ़ॉर्म का उपयोग करें।
निष्कर्ष में
इस प्रकार, समरूपता का गुणांक कई विशेषज्ञों की राय की निरंतरता को दर्शाता है। यह 0 से जितना दूर है और 1 के करीब है, उतनी ही सुसंगत राय है। पियर्सन मानदंड की गणना करके इन गुणांकों की पुष्टि की जानी चाहिए।






