ऊष्मप्रवैगिकी का एक महत्वपूर्ण खंड किसी पदार्थ के विभिन्न चरणों के बीच परिवर्तनों का अध्ययन है, क्योंकि ये प्रक्रियाएं व्यवहार में होती हैं और कुछ शर्तों के तहत एक प्रणाली के व्यवहार की भविष्यवाणी करने के लिए मौलिक महत्व की होती हैं। इन परिवर्तनों को चरण संक्रमण कहा जाता है, जिसके लिए लेख समर्पित है।
एक चरण और एक सिस्टम घटक की अवधारणा

भौतिकी में चरण संक्रमण पर विचार करने से पहले, चरण की अवधारणा को ही परिभाषित करना आवश्यक है। जैसा कि सामान्य भौतिकी के पाठ्यक्रम से जाना जाता है, पदार्थ की तीन अवस्थाएँ होती हैं: गैसीय, ठोस और तरल। विज्ञान के एक विशेष खंड में - ऊष्मप्रवैगिकी में - नियम पदार्थ के चरणों के लिए तैयार किए जाते हैं, न कि उनके एकत्रीकरण के राज्यों के लिए। एक चरण को पदार्थ की एक निश्चित मात्रा के रूप में समझा जाता है जिसमें एक सजातीय संरचना होती है, जो विशिष्ट भौतिक और रासायनिक गुणों की विशेषता होती है और शेष पदार्थ से सीमाओं से अलग होती है, जिसे इंटरफेज़ कहा जाता है।
इस प्रकार, "चरण" की अवधारणा गुणों के बारे में अधिक व्यावहारिक रूप से महत्वपूर्ण जानकारी रखती हैइसके एकत्रीकरण की स्थिति की तुलना में मामला। उदाहरण के लिए, लोहे जैसी धातु की ठोस अवस्था निम्न चरणों में हो सकती है: निम्न-तापमान चुंबकीय शरीर-केंद्रित घन (BCC), निम्न-तापमान गैर-चुंबकीय bcc, चेहरा-केंद्रित घन (fcc), और उच्च- तापमान गैर-चुंबकीय बीसीसी।
"चरण" की अवधारणा के अलावा, थर्मोडायनामिक्स के नियम भी "घटक" शब्द का उपयोग करते हैं, जिसका अर्थ है कि एक विशेष प्रणाली बनाने वाले रासायनिक तत्वों की संख्या। इसका मतलब है कि चरण या तो मोनोकंपोनेंट (1 रासायनिक तत्व) या मल्टीकंपोनेंट (कई रासायनिक तत्व) हो सकता है।
गिब्स प्रमेय और प्रणाली के चरणों के बीच संतुलन

चरण परिवर्तन को समझने के लिए उनके बीच संतुलन की स्थिति जानना आवश्यक है। इन शर्तों को गणितीय रूप से उनमें से प्रत्येक के लिए गिब्स समीकरणों की प्रणाली को हल करके प्राप्त किया जा सकता है, यह मानते हुए कि संतुलन की स्थिति तब पहुंच जाती है जब बाहरी प्रभाव से पृथक सिस्टम की कुल गिब्स ऊर्जा बदलना बंद हो जाती है।
समीकरणों की संकेतित प्रणाली को हल करने के परिणामस्वरूप, कई चरणों के बीच संतुलन के अस्तित्व के लिए स्थितियां प्राप्त होती हैं: एक पृथक प्रणाली केवल तभी विकसित होगी जब प्रत्येक घटक के दबाव, रासायनिक क्षमता और सभी चरणों में तापमान एक दूसरे के बराबर हैं।
संतुलन के लिए गिब्स चरण नियम

कई चरणों और घटकों से युक्त एक प्रणाली न केवल संतुलन में हो सकती हैकुछ शर्तों के तहत, उदाहरण के लिए, एक विशिष्ट तापमान और दबाव पर। संतुलन के लिए गिब्स प्रमेय में कुछ चर को चरणों की संख्या और इस संतुलन में मौजूद घटकों की संख्या दोनों को बनाए रखते हुए बदला जा सकता है। प्रणाली में संतुलन को भंग किए बिना चरों की संख्या को बदला जा सकता है, इस प्रणाली की स्वतंत्रता की संख्या कहलाती है।
f चरणों और k घटकों वाली प्रणाली की स्वतंत्रता l की संख्या विशिष्ट रूप से गिब्स चरण नियम से निर्धारित होती है। यह नियम गणितीय रूप से इस प्रकार लिखा गया है: l + f=k + 2. इस नियम के साथ कैसे कार्य करें? बहुत आसान। उदाहरण के लिए, यह ज्ञात है कि प्रणाली में f=3 संतुलन चरण होते हैं। ऐसी प्रणाली में कम से कम कितने घटक हो सकते हैं? आप इस प्रश्न का उत्तर निम्न प्रकार से तर्क द्वारा दे सकते हैं: संतुलन के मामले में, सबसे कठोर परिस्थितियाँ तब मौजूद होती हैं जब इसे केवल कुछ संकेतकों पर महसूस किया जाता है, अर्थात, किसी भी थर्मोडायनामिक पैरामीटर में बदलाव से असंतुलन होगा। इसका मतलब है कि स्वतंत्रता की संख्या एल=0। एल और एफ के ज्ञात मूल्यों को प्रतिस्थापित करते हुए, हम के=1 प्राप्त करते हैं, अर्थात, एक प्रणाली जिसमें तीन चरण संतुलन में हैं, में एक घटक शामिल हो सकता है। एक प्रमुख उदाहरण पानी का त्रिगुण बिंदु है, जहां बर्फ, तरल पानी और भाप विशिष्ट तापमान और दबाव पर संतुलन में मौजूद हैं।
चरण परिवर्तन का वर्गीकरण
यदि आप संतुलन में एक प्रणाली में कुछ थर्मोडायनामिक मापदंडों को बदलना शुरू करते हैं, तो आप देख सकते हैं कि एक चरण कैसे गायब हो जाएगा और दूसरा कैसे दिखाई देगा। इस प्रक्रिया का एक सरल उदाहरण बर्फ को गर्म करने पर पिघलना है।
यह देखते हुए कि गिब्स समीकरण केवल दो चर (दबाव और तापमान) पर निर्भर करता है, और चरण संक्रमण में इन चरों में परिवर्तन शामिल है, तो गणितीय रूप से चरणों के बीच संक्रमण को गिब्स ऊर्जा के संबंध में अंतर करके वर्णित किया जा सकता है चर। 1933 में ऑस्ट्रियाई भौतिक विज्ञानी पॉल एरेनफेस्ट द्वारा इस दृष्टिकोण का उपयोग किया गया था, जब उन्होंने चरण संतुलन में बदलाव के साथ होने वाली सभी ज्ञात थर्मोडायनामिक प्रक्रियाओं का एक वर्गीकरण संकलित किया था।
ऊष्मप्रवैगिकी की मूल बातें से यह निम्नानुसार है कि तापमान के संबंध में गिब्स ऊर्जा का पहला व्युत्पन्न प्रणाली के एन्ट्रॉपी में परिवर्तन के बराबर है। दबाव के संबंध में गिब्स ऊर्जा का व्युत्पन्न आयतन में परिवर्तन के बराबर है। यदि, जब सिस्टम में चरण बदलते हैं, एन्ट्रापी या वॉल्यूम में विराम होता है, यानी वे अचानक बदल जाते हैं, तो वे पहले क्रम के चरण संक्रमण की बात करते हैं।
इसके अलावा, तापमान और दबाव के संबंध में गिब्स ऊर्जा का दूसरा व्युत्पन्न क्रमशः ताप क्षमता और वॉल्यूमेट्रिक विस्तार का गुणांक है। यदि चरणों के बीच परिवर्तन संकेतित भौतिक मात्राओं के मूल्यों में एक असंतुलन के साथ होता है, तो एक दूसरे क्रम के चरण संक्रमण की बात करता है।
चरणों के बीच परिवर्तन के उदाहरण

प्रकृति में विभिन्न संक्रमणों की एक बड़ी संख्या है। इस वर्गीकरण के ढांचे के भीतर, पहली तरह के संक्रमणों के हड़ताली उदाहरण धातुओं के पिघलने या हवा से जल वाष्प के संघनन की प्रक्रियाएं हैं, जब सिस्टम में मात्रा में उछाल होता है।
अगर हम दूसरे क्रम के संक्रमणों के बारे में बात करते हैं, तो एक तापमान पर लोहे का चुंबकीय से एक अनुचुंबकीय अवस्था में परिवर्तन के हड़ताली उदाहरण हैं768 C या धात्विक चालक का निरपेक्ष शून्य के करीब तापमान पर अतिचालक अवस्था में परिवर्तन।
पहले प्रकार के संक्रमणों का वर्णन करने वाले समीकरण
व्यवहार में, यह जानना अक्सर आवश्यक होता है कि किसी सिस्टम में चरण परिवर्तन होने पर तापमान, दबाव और अवशोषित (मुक्त) ऊर्जा कैसे बदलती है। इस उद्देश्य के लिए दो महत्वपूर्ण समीकरणों का उपयोग किया जाता है। वे ऊष्मप्रवैगिकी की मूल बातों के ज्ञान के आधार पर प्राप्त किए जाते हैं:
- क्लैपेरॉन का सूत्र, जो विभिन्न चरणों के बीच परिवर्तन के दौरान दबाव और तापमान के बीच संबंध स्थापित करता है।
- क्लॉसियस सूत्र जो परिवर्तन के दौरान अवशोषित (मुक्त) ऊर्जा और सिस्टम के तापमान को जोड़ता है।
दोनों समीकरणों का उपयोग न केवल भौतिक मात्राओं की मात्रात्मक निर्भरता प्राप्त करने में है, बल्कि चरण आरेखों पर संतुलन वक्रों के ढलान के संकेत को निर्धारित करने में भी है।
दूसरे प्रकार के संक्रमणों का वर्णन करने के लिए समीकरण

पहली और दूसरी तरह के चरण संक्रमणों को अलग-अलग समीकरणों द्वारा वर्णित किया गया है, क्योंकि दूसरे क्रम के संक्रमणों के लिए क्लॉसियस और क्लॉसियस समीकरणों के आवेदन से गणितीय अनिश्चितता होती है।
उत्तरार्द्ध का वर्णन करने के लिए, एरेनफेस्ट समीकरणों का उपयोग किया जाता है, जो परिवर्तन प्रक्रिया के दौरान ताप क्षमता में परिवर्तन और वॉल्यूमेट्रिक विस्तार के गुणांक के ज्ञान के माध्यम से दबाव और तापमान में परिवर्तन के बीच संबंध स्थापित करते हैं। चुंबकीय क्षेत्र की अनुपस्थिति में कंडक्टर-सुपरकंडक्टर संक्रमणों का वर्णन करने के लिए एरेनफेस्ट समीकरणों का उपयोग किया जाता है।
महत्वचरण आरेख
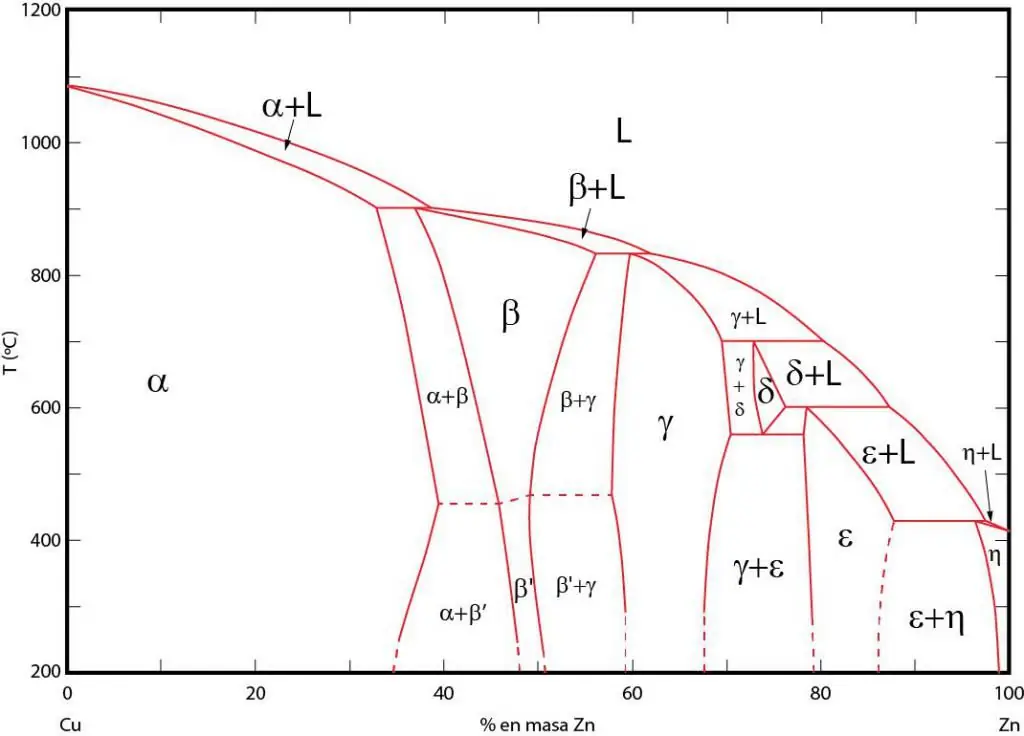
फेज आरेख उन क्षेत्रों का एक ग्राफिक प्रतिनिधित्व है जिसमें संबंधित चरण संतुलन में मौजूद हैं। इन क्षेत्रों को चरणों के बीच संतुलन रेखाओं द्वारा अलग किया जाता है। P-T (दबाव-तापमान), T-V (तापमान-मात्रा), और P-V (दबाव-मात्रा) चरण आरेख अक्सर उपयोग किए जाते हैं।
चरण आरेखों का महत्व इस तथ्य में निहित है कि वे आपको यह अनुमान लगाने की अनुमति देते हैं कि बाहरी परिस्थितियों में तदनुसार परिवर्तन होने पर सिस्टम किस चरण में होगा। वांछित गुणों वाली संरचना प्राप्त करने के लिए इस जानकारी का उपयोग विभिन्न सामग्रियों के ताप उपचार में किया जाता है।






